题目内容
6.已知f(x)是定义在R上的偶函数,f(1)=1,且对任意x∈R都有f(x+4)=f(x),则f(99)等于( )| A. | -1 | B. | 0 | C. | 1 | D. | 99 |
分析 由已知推导出f(99)=f(4×25-1)=f(-1)=f(1),由此能求出结果.
解答 解:∵f(x)是定义在R上的偶函数,f(1)=1,
且对任意x∈R都有f(x+4)=f(x),
∴f(99)=f(4×25-1)=f(-1)=f(1)=1.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
1.函数y=|x-1|+1可表示为( )
| A. | $y=\left\{{\begin{array}{l}{2-x,x<1}\\{x,x>1}\end{array}}\right.$ | B. | $y=\left\{{\begin{array}{l}{2-x,x>1}\\{x,x≤1}\end{array}}\right.$ | C. | $y=\left\{{\begin{array}{l}{x,x<1}\\{2-x,x≥1}\end{array}}\right.$ | D. | $y=\left\{{\begin{array}{l}{2-x,x<1}\\{x,x≥1}\end{array}}\right.$ |
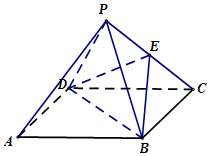 如图,在正四棱锥P-ABCD中,PA=AB=a,E是棱PC的中点.
如图,在正四棱锥P-ABCD中,PA=AB=a,E是棱PC的中点.