题目内容
11．已知函数$f（x）=\left\{{\begin{array}{l}{{2^x}+1，x＜2}\\{{x^2}+px，x≥2}\end{array}}\right.$，若f（f（0））=5p，则p的值为$\frac{4}{3}$．分析 先求出f（0）=20+1=2，从而f（f（0））=f（2）=22+2p=5p，由此能求出p的值．
解答 解：∵函数$f（x）=\left\{{\begin{array}{l}{{2^x}+1，x＜2}\\{{x^2}+px，x≥2}\end{array}}\right.$，f（f（0））=5p，
∴f（0）=20+1=2，
f（f（0））=f（2）=22+2p=5p，
解得p=$\frac{4}{3}$．
故答案为：$\frac{4}{3}$．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
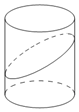一个底面半径为2的圆柱被与其底面所成角是60°的平面所截，截面是一个椭圆，则该椭圆的焦距等于$4\sqrt{3}$．
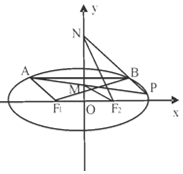如图，F1，F2分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，且焦距为2$\sqrt{2}$，动弦AB平行于x轴，且|F1A|+|F1B|=4．
3．若$sin（\frac{π}{6}-α）=\frac{1}{3}$，则${cos^2}（\frac{π}{6}+\frac{α}{2}）$=（ ）
| A． | $\frac{7}{9}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $-\frac{7}{9}$ |