题目内容
已知Z为整数集,集合U={x∈Z|x2-6x≥0},集合M满足M⊆∁ZU,且M∩{1,2,3}={1,2},则M的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:交集及其运算
专题:集合
分析:求出U中不等式的解集,找出解集的整数解确定出U,根据全集Z求出U的补集,根据M为U补集的子集,且M∩{1,2,3}={1,2},确定出M个数即可.
解答:
解:由U中的不等式变形得:x(x-6)≥0,
解得:x≤0或x≥6,即U={x∈Z|x≤0或x≥6},
∵全集为Z,
∴∁ZU={x∈Z|0<x<6}={1,2,3,4,5},
∵M⊆∁ZU,且M∩{1,2,3}={1,2},
∴M={1,2};{1,2,3};{1,2,4};{1,2,5}共4个,
故选:D
解得:x≤0或x≥6,即U={x∈Z|x≤0或x≥6},
∵全集为Z,
∴∁ZU={x∈Z|0<x<6}={1,2,3,4,5},
∵M⊆∁ZU,且M∩{1,2,3}={1,2},
∴M={1,2};{1,2,3};{1,2,4};{1,2,5}共4个,
故选:D
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
设α,β是方程x2-8x+k2=0的两根,且α,αβ,β成等差数列,则k=( )
| A、2 | B、4 | C、±2 | D、±4 |
若实数x,y满足条件
,则x+2y的最小值等于( )
|
| A、3 | B、4 | C、5 | D、9 |
已知数列1,a1,a2,9成等差数列,1,b1,b2,b3,9成等比数列,则
=( )
| a1+a2 |
| b2 |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、±
|
不等式-x2+x+2≥0的解集是( )
| A、[-1,2] |
| B、(-∞,-1]∪[2,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪[1,+∞) |
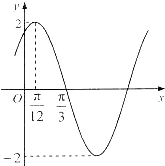
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
)的部分图象如图所示,则( )
| π |
| 2 |

A、ω=2,φ=
| ||||
B、ω=
| ||||
C、ω=2,φ=
| ||||
D、ω=
|