题目内容
已知函数f(x)=ln(ex+a)(a为常数)是R上的奇函数,函数g(x)=λf(x)+sinx是区间[-1,1]上的减函数
(1)求a的值
(2)讨论关于x的方程
=x2-2ex+m的根的函数
(3)若g(x)<t2+λt+1在x∈[-1,1]上恒成立,求t的取值范围.
(1)求a的值
(2)讨论关于x的方程
| lnx |
| f(x) |
(3)若g(x)<t2+λt+1在x∈[-1,1]上恒成立,求t的取值范围.
考点:函数恒成立问题,利用导数求闭区间上函数的最值
专题:
分析:(1)直接根据函数f(x)=ln(ex+a)是实数集R上的奇函数,则f(0)=0,即可求出a的取值;
(2)构造两个函数f1(x)=
,f2(x)=x2-2ex+m,将方程有根的问题转化为函数有交点的问题进行研究.
(3)先利用函数g(x)在[-1,1]上单调递减,求出其最大值,再把g(x)<t2-λt+1在x∈[-1,1]上恒成立转化为其最大值小于等于t2-λt+1恒成立,进而得到(1-t)λ+t2+sin1+1≥0(其中λ≤-1)恒成立,再利用二次函数恒成立问题的解法即可求t出的取值范围.
(2)构造两个函数f1(x)=
| lnx |
| x |
(3)先利用函数g(x)在[-1,1]上单调递减,求出其最大值,再把g(x)<t2-λt+1在x∈[-1,1]上恒成立转化为其最大值小于等于t2-λt+1恒成立,进而得到(1-t)λ+t2+sin1+1≥0(其中λ≤-1)恒成立,再利用二次函数恒成立问题的解法即可求t出的取值范围.
解答:
解:(1)∵函数f(x)=ln(ex+a)是实数集R上的奇函数,
∴f(0)=0,即ln(1+a)=0,
∴a=0.
(2)当a=0时,f(x)=ln(ex+a)=f(x)=lnex=x,
由程
=x2-2ex+m得
=x2-2ex+m,
令f1(x)=
,f2(x)=x2-2ex+m,
∵f′1(x)=
,
当x∈(0,e)时,f′1(x)>0,
∴f1(x)在(0,e]上为增函数;
当x∈(e,+∞)时,f′1(x)<0,
∴f1(x)在(e,+∞)上为减函数;
∴当x=e时,[f1(x)]max=f1(e)=
.
而f2(x)=(x-e)2+m-e2,
∴当m-e2>
时,即m>e2+
时方程无解.
当m-e2=
时,即m=e2+
时方程有一解.
当m-e2<
时,即m<e2+
时方程有两解.
(3)由题意可得:g(x)=λx+sinx,
∴g'(x)=λ+cosx,由函数的单调性转化为:g'(x)=λ+cosx≤0在[-1,1]上恒成立,
进而得到λ≤-1,g(x)max=-λ-sin1,
再转化为-λ-sin1<t2+λt+1在λ∈(-∞,-1]上恒成立.
∴(t+1)λ+t2+sin1+1>0在λ∈(-∞,-1]上恒成立.
令h(λ)=(t+1)λ+t2+sin1+1,(λ≤-1)
则
,
∴
,
而t<-1时,t2-t+sin1>0恒成立,
经检验t=-1也对,
∴t≤-1.
∴f(0)=0,即ln(1+a)=0,
∴a=0.
(2)当a=0时,f(x)=ln(ex+a)=f(x)=lnex=x,
由程
| lnx |
| f(x) |
| ln?x |
| x |
令f1(x)=
| ln?x |
| x |
∵f′1(x)=
| 1-lnx |
| x2 |
当x∈(0,e)时,f′1(x)>0,
∴f1(x)在(0,e]上为增函数;
当x∈(e,+∞)时,f′1(x)<0,
∴f1(x)在(e,+∞)上为减函数;
∴当x=e时,[f1(x)]max=f1(e)=
| 1 |
| e |
而f2(x)=(x-e)2+m-e2,
∴当m-e2>
| 1 |
| e |
| 1 |
| e |
当m-e2=
| 1 |
| e |
| 1 |
| e |
当m-e2<
| 1 |
| e |
| 1 |
| e |
(3)由题意可得:g(x)=λx+sinx,
∴g'(x)=λ+cosx,由函数的单调性转化为:g'(x)=λ+cosx≤0在[-1,1]上恒成立,
进而得到λ≤-1,g(x)max=-λ-sin1,
再转化为-λ-sin1<t2+λt+1在λ∈(-∞,-1]上恒成立.
∴(t+1)λ+t2+sin1+1>0在λ∈(-∞,-1]上恒成立.
令h(λ)=(t+1)λ+t2+sin1+1,(λ≤-1)
则
|
∴
|
而t<-1时,t2-t+sin1>0恒成立,
经检验t=-1也对,
∴t≤-1.
点评:本题考查导数知识的运用,考查函数的单调性,将不等式恒成立问题,转化为求函数最值问题,考查学生的运算能力,综合性较强,运算量较大.

练习册系列答案
相关题目
已知集合A={x|-2≤x≤2},B={x|0<x<1},则有( )
| A、A>B | B、A?B |
| C、B?A | D、A⊆B |
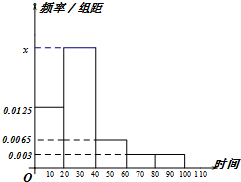 某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].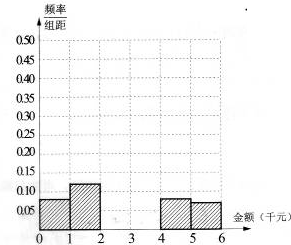 某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表:
某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表: