题目内容
已知函数f(x)=x2,g(x)=x-1.
(1)若不等式f(x)>bg(x)对任意的实数x恒成立,求实数b的取值范围;
(2)设F(x)=f(x)-mg(x)+1-m-m2,且|F(x)|在[0,1]上单调递增,求实数m的取值范围.
(1)若不等式f(x)>bg(x)对任意的实数x恒成立,求实数b的取值范围;
(2)设F(x)=f(x)-mg(x)+1-m-m2,且|F(x)|在[0,1]上单调递增,求实数m的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:(1)将不等式恒成立转化为x2-bx+b>0,再利用二次函数的性质得△<0,即可解出实数b的取值范围;
(2)先求得F(x)=x2-mx+1-m2,再对其对应方程的判别式分△≤0和当△>0两种情况,分别找到满足|F(x)|在[0,1]上单调递增的实数m的取值范围,最后综合即可.
(2)先求得F(x)=x2-mx+1-m2,再对其对应方程的判别式分△≤0和当△>0两种情况,分别找到满足|F(x)|在[0,1]上单调递增的实数m的取值范围,最后综合即可.
解答:
解:(1)∵f(x)=x2,g(x)=x-1.
∴若不等式f(x)>bg(x)对任意的实数x恒成立,
等价为x2-bx+b>0恒成立,
∴△=b2-4b<0,
解得0<b<4,
∴实数b的取值范围是(0,4);
(2)由题设得F(x)=x2-mx+1-m2,
对称轴方程为x=
,△=m2-4(1-m2)=5m2-4,
由于|F(x)|在[0,1]上单调递增,则有:
①当△≤0,即-
≤m≤
时,有
,
解得-
≤m≤0,
②当△>0,即m<-
或m>
时,
设方程F(x)=0的根为x1,x2(x1<x2),
若m>
,则
>
,
有
,
解得m≥2;
若m<-
,即
<-
,
有x1<0,x2≤0;
得F(0)=1-m2≥0,
即-1≤m≤1,
∴-1≤m<-
,
综上所述,实数m的取值范围是[-1,0]∪[2,+∞).
∴若不等式f(x)>bg(x)对任意的实数x恒成立,
等价为x2-bx+b>0恒成立,
∴△=b2-4b<0,
解得0<b<4,
∴实数b的取值范围是(0,4);
(2)由题设得F(x)=x2-mx+1-m2,
对称轴方程为x=
| m |
| 2 |
由于|F(x)|在[0,1]上单调递增,则有:
①当△≤0,即-
2
| ||
| 5 |
2
| ||
| 5 |
|
解得-
2
| ||
| 5 |
②当△>0,即m<-
2
| ||
| 5 |
2
| ||
| 5 |
设方程F(x)=0的根为x1,x2(x1<x2),
若m>
2
| ||
| 5 |
| m |
| 2 |
| ||
| 5 |
有
|
解得m≥2;
若m<-
2
| ||
| 5 |
| m |
| 2 |
| ||
| 5 |
有x1<0,x2≤0;
得F(0)=1-m2≥0,
即-1≤m≤1,
∴-1≤m<-
2
| ||
| 5 |
综上所述,实数m的取值范围是[-1,0]∪[2,+∞).
点评:本题主要考查二次函数的图象和性质,以及不等式恒成立问题,综合性较强,运算量较大,考查分类讨论的数学思想.

练习册系列答案
相关题目
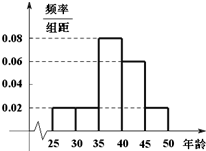 某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表. 参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题:
参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题: