题目内容
设f(x)与g(x)是定义在同一区间D上的两个函数,若?x0∈D,使得|f(x0)-g(x0)|≤1,则称f(x)和g(x)是D上的“接近函数”,D称为“接近区间”;若?x∈D,都有|f(x)-g(x)|>1,则称f(x)和g(x)是D上的“远离函数”,D称为“远离区间”.给出以下命题:
①f(x)=x2+1与g(x)=x2+
是(-∞,+∞)上的“接近函数”;
②f(x)=x2-3x+4与g(x)=2x-3的一个“远离区间”可以是[2,3];
③f(x)=
和g(x)=-x+b(b>
)是(-1,1)上的“接近函数”,则
<b≤
+1;
④若f(x)=
+2ex与g(x)=x2+a+e2(e是自然对数的底数)是[1,+∞)上的“远离函数”,则a>1+
.
其中的真命题有 .(写出所有真命题的序号)
①f(x)=x2+1与g(x)=x2+
| 3 |
| 2 |
②f(x)=x2-3x+4与g(x)=2x-3的一个“远离区间”可以是[2,3];
③f(x)=
| 1-x2 |
| 2 |
| 2 |
| 2 |
④若f(x)=
| lnx |
| x |
| ||
| e |
其中的真命题有
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:根据已知中“接近函数”和“远离函数”的定义,逐一分析题目中给定的四组函数是否符号定义,最后综合讨论结果,可得答案.
解答:
解:对于①,若f(x)=x2+1与g(x)=x2+
,则|f(x0)-g(x0)|=1恒成立,
故f(x)=x2+1与g(x)=x2+
是(-∞,+∞)上的“接近函数”;
故①正确;
对于②,若f(x)=x2-3x+4与g(x)=2x-3,
则|f(x0)-g(x0)|=|x02-5x0+7|=|(x0-
)2+
|,
当x0∈[2,3]时,|f(x0)-g(x0)|≤1恒成立,
故[2,3]是f(x)=x2-3x+4与g(x)=2x-3的一个“接近区间”,
故②错误;
对于③,若f(x)=
和g(x)=-x+b(b>
)是(-1,1)上的“接近函数”,
则?x∈(-1,1)使|f(x)-g(x)|≤1,
即?x∈(-1,1)使-x+b-
≤1,
即?x∈(-1,1)使b≤(
+1+x)max,
令h(x)=
+1+x,则h′(x)=1-
,
则当x∈(-
,
)时,h′(x)>0,h(x)为增函数;当x∈(
,1)时,h′(x)<0,h(x)为减函数;
故当x=
时,h(x)取最大值
+1,
则
<b≤
+1;
故③正确;
④若f(x)=
+2ex与g(x)=x2+a+e2(e是自然对数的底数)是[1,+∞)上的“远离函数”,
即?x∈[1,+∞),
|
+2ex-x2-a-e2|=|a-
-2ex+x2+e2|=|(x-e)2+a-
|>1,
令p(x)=(x-e)2+a,则p(x)在(-∞,e)上递减,在(e,+∞)上递增,
∴当x=e时,p(x)取最小值a;
令q(x)=
,则q′(x)=
,易得q(x)在(-∞,e)上递增,在(e,+∞)上递减,
∴当x=e时,p(x)取最大值
;
∴|(x-e)2+a-
|min=|a-
|>1,
即a>1+
或a<-1+
.
故④错误;
故真命题有:①③,
故答案为:①③.
| 3 |
| 2 |
故f(x)=x2+1与g(x)=x2+
| 3 |
| 2 |
故①正确;
对于②,若f(x)=x2-3x+4与g(x)=2x-3,
则|f(x0)-g(x0)|=|x02-5x0+7|=|(x0-
| 5 |
| 2 |
| 3 |
| 4 |
当x0∈[2,3]时,|f(x0)-g(x0)|≤1恒成立,
故[2,3]是f(x)=x2-3x+4与g(x)=2x-3的一个“接近区间”,
故②错误;
对于③,若f(x)=
| 1-x2 |
| 2 |
则?x∈(-1,1)使|f(x)-g(x)|≤1,
即?x∈(-1,1)使-x+b-
| 1-x2 |
即?x∈(-1,1)使b≤(
| 1-x2 |
令h(x)=
| 1-x2 |
| x | ||
|
则当x∈(-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
故当x=
| ||
| 2 |
| 2 |
则
| 2 |
| 2 |
故③正确;
④若f(x)=
| lnx |
| x |
即?x∈[1,+∞),
|
| lnx |
| x |
| lnx |
| x |
| lnx |
| x |
令p(x)=(x-e)2+a,则p(x)在(-∞,e)上递减,在(e,+∞)上递增,
∴当x=e时,p(x)取最小值a;
令q(x)=
| lnx |
| x |
| 1-lnx |
| x2 |
∴当x=e时,p(x)取最大值
| 1 |
| e |
∴|(x-e)2+a-
| lnx |
| x |
| 1 |
| e |
即a>1+
| 1 |
| e |
| 1 |
| e |
故④错误;
故真命题有:①③,
故答案为:①③.
点评:本题考查的知识点是命题的真假判断与应用,其中正确理解“接近函数”和“远离函数”的定义,是解答的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
为了保护环境,发展低碳经济,甲、乙两企业在国家科研部门的支持下,进行技术攻关,采用新工艺,减少二氧化碳排放量.已知从2009年6月起至2010年3月止,两企业每月的减排量如右图所示,则甲、乙两企业在这10个月内月平均减排量分别为( )
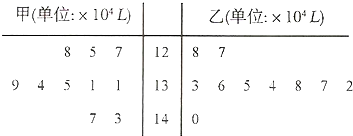

| A、133,133 |
| B、134,133 |
| C、134,134 |
| D、1343,134 |
cos
的值是( )
| 31π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|