题目内容

已知函数f（x）=
|log5(1-x)|(x＜1)
-(x-2)2+2(x≥1)
，则关于x的方程f（|x|）=a的实数个数不可能为（　　）
A、3个B、4个C、5个D、6个
考点：根的存在性及根的个数判断
专题：计算题,作图题,函数的性质及应用
分析：关于x的方程f（|x|）=a的实数个数可由函数y=f（|x|）的图象作出，从而解得．
解答： 解：作函数y=f（|x|）的图象如下，

由图可知，当a=0时，有三个根，
当a=2时，有四个根，
当1＜a＜2时，有6个根，
没有5个根的情况，
故选C．
点评：本题考查了函数的零点与方程的根的联系与应用，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=2aex（a＞0，e为自然对数的底数）的图象与直线x=0的交点为M，函数g（x）=ln
x
a
（a＞0）的图象与直线y=0的交点为N，|MN|恰好是点M到函数g（x）=ln
x
a
（a＞0）图象上的最小值，则实数a的值是
 
．
已知函数f（x）=loga
2m-x
2+x
（a＞0，且a≠1）为奇函数，且f（1）=-1．
（1）求实数a与m的值；
（2）用定义证明函数f（x）的单调性；
（3）解不等式f（
1
2x
）+1＜0．
设函数g（x）=sin（
π
4
x-
π
6
）-2cos2（
π
8
x）+1．
（1）求f（x）的对称中心，对称轴，单调增区间．
（2）若函数y=g（x）与y=f（x）的图象关于直线x=1对称，求当x∈[0，
4
3
]时y=g（x）的最大值．
已知数列{an}是等差数列，从a1，a2，a3，a4，a5，a6，a7中取走任意四项，则剩下三项构成等差数列的概率为（　　）
A、
6
35
B、
9
35
C、1或
9
35
D、1或
6
35
已知在长方形ABCD中，AB=2，BC=1，在长方形ABCD中任取一点P，求∠APB＜∠90°的概率．
为了保护环境，发展低碳经济，甲、乙两企业在国家科研部门的支持下，进行技术攻关，采用新工艺，减少二氧化碳排放量．已知从2009年6月起至2010年3月止，两企业每月的减排量如右图所示，则甲、乙两企业在这10个月内月平均减排量分别为（　　）
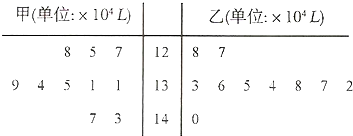
A、133，133
B、134，133
C、134，134
D、1343，134
在（x-2）5（
2
+y）4的展开式中，x3y2的系数为
 
．
已知点F是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点，抛物线y2=4cx（c＞0）的准线交该双曲线于A，B两点，若△ABF是锐角三角形且c2=a2+b2，则该双曲线离心率e的取值范围是（　　）
A、(1，
3
)
B、(1+
2
，+∞)
C、(
3
，2
2
)
D、(1，1+
2
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网