题目内容
已知曲线Γ上的点到点F(0,1)的距离比它到直线y=-3的距离小2.
(Ⅰ)求曲线Γ的方程;
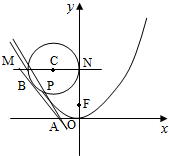
(Ⅱ)曲线Γ在点P处的切线l与x轴交于点A.直线y=3分别与直线l及y轴交于点M,N,以MN为直径作圆C,过点A作圆C的切线,切点为B,试探究:当点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度是否发生变化?证明你的结论.
(Ⅰ)求曲线Γ的方程;
(Ⅱ)曲线Γ在点P处的切线l与x轴交于点A.直线y=3分别与直线l及y轴交于点M,N,以MN为直径作圆C,过点A作圆C的切线,切点为B,试探究:当点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度是否发生变化?证明你的结论.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设S(x,y)曲线Γ上的任意一点,利用抛物线的定义,判断S满足配额我想的定义,即可求曲线Γ的方程;
(Ⅱ)通过抛物线方程利用函数的导数求出切线方程,求出A、M的坐标,N的坐标,以MN为直径作圆C,求出圆心坐标,半径是常数,即可证明当点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度不变.
(Ⅱ)通过抛物线方程利用函数的导数求出切线方程,求出A、M的坐标,N的坐标,以MN为直径作圆C,求出圆心坐标,半径是常数,即可证明当点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度不变.
解答:
 解:(Ⅰ)设S(x,y)曲线Γ上的任意一点,
解:(Ⅰ)设S(x,y)曲线Γ上的任意一点,
由题意可得:点S到F(0,1)的距离与它到直线y=-1的距离相等,
曲线Γ是以F为焦点直线y=-1为准线的抛物线,
∴曲线Γ的方程为:x2=4y.
(Ⅱ)当点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度不变,
证明如下:由(Ⅰ)可知抛物线的方程为y=
x2,
设P(x0,y0)(x0≠0)则y0=
x02,
由y′=
x得切线l的斜率k=y′
=
x0
∴切线l的方程为:y-y0=
x0(x-x0),即y=
x0x-
x02.
由
得A(
x0,0),
由
得M(
x0+
,3),
又N(0,3),
所以圆心C(
x0+
,3),半径r=
|MN|=|
x0+
||AB|=
=
=
∴点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度不变.
 解:(Ⅰ)设S(x,y)曲线Γ上的任意一点,
解:(Ⅰ)设S(x,y)曲线Γ上的任意一点,由题意可得:点S到F(0,1)的距离与它到直线y=-1的距离相等,
曲线Γ是以F为焦点直线y=-1为准线的抛物线,
∴曲线Γ的方程为:x2=4y.
(Ⅱ)当点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度不变,
证明如下:由(Ⅰ)可知抛物线的方程为y=
| 1 |
| 4 |
设P(x0,y0)(x0≠0)则y0=
| 1 |
| 4 |
由y′=
| 1 |
| 2 |
| | | x=x0 |
| 1 |
| 2 |
∴切线l的方程为:y-y0=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
由
|
| 1 |
| 2 |
由
|
| 1 |
| 2 |
| 6 |
| x0 |
又N(0,3),
所以圆心C(
| 1 |
| 4 |
| 3 |
| x0 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| x0 |
| |AC|2-r2 |
[
|
| 6 |
∴点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度不变.
点评:本题考查轨迹方程的求法,直线与抛物线的位置关系的应用,圆的方程函数的导数等指数的应用,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义由如图框图表示的运算,若f(x)=|x+1|+|x-1|,则输出y=( )
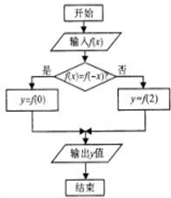

| A、0 | B、1 | C、2 | D、4 |