题目内容
正四棱锥P-ABCD的所有棱长都相等，则侧棱与底面所成的角为 ．
考点：棱锥的结构特征
专题：空间角
分析：连结AC，BD交于点O，连结PO，PO⊥底面ABCD，所以∠PAC就是侧棱与底面所成角，由此能求出侧棱与底面所成角的大小．
解答：
解：连结AC，BD交于点O，连结PO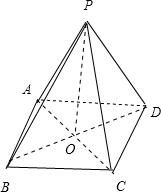
则由正棱锥性质可知PO是正四棱锥P-ABCD底面上的高
即PO⊥底面ABCD
所以∠PAC就是侧棱与底面所成角
设正四棱锥P-ABCD的各条棱长均为a
则在底面正方形中，对角线AC=（根号2）a
又PA=PC=a，则在△PAC中：
PA2+PC2=2a2=AC2，满足勾股定理
所以△PAC是等腰直角三角形，
那么∠PAC=45°
即侧棱与底面所成角的大小为45°．
故答案为：45°．
则由正棱锥性质可知PO是正四棱锥P-ABCD底面上的高
即PO⊥底面ABCD
所以∠PAC就是侧棱与底面所成角
设正四棱锥P-ABCD的各条棱长均为a
则在底面正方形中，对角线AC=（根号2）a
又PA=PC=a，则在△PAC中：
PA2+PC2=2a2=AC2，满足勾股定理
所以△PAC是等腰直角三角形，
那么∠PAC=45°
即侧棱与底面所成角的大小为45°．
故答案为：45°．
点评：本题考查侧棱与底面所成角的大小的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
如图所示，一根水平放置的长方体枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比．