题目内容
已知方程mx+3m=
有两个不同的实数解，则实数m的取值范围是 ．
| 4-x2 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：构造函数g（x）=mx+3m=m（x+3），f（x）=
，在同一坐标系中作出二函数的图象，数形结合即可求得实数m的取值范围．
| 4-x2 |
解答：
解：令g（x）=mx+3m=m（x+3），f（x）=
，
∵方程mx+3m=
有两个不同的实数解，
∴g（x）=mx+3m=m（x+3）与f（x）=
有两个不同的交点，
在同一坐标系中作图如下：
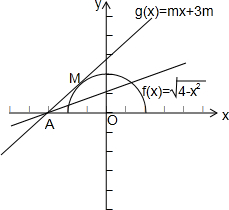
∵g（x）=mx+3m=m（x+3）为过定点（-3，0）的直线，
∴m=0时，显然g（x）=0与f（x）=
有两个不同的交点；
当直线g（x）=mx+3m与曲线f（x）=
相切时，
=2，解得m=
=
或m=-
（舍），
∴0≤m＜
，即实数m的取值范围是[0，
）．
故答案为：[0，
）．
| 4-x2 |
∵方程mx+3m=
| 4-x2 |
∴g（x）=mx+3m=m（x+3）与f（x）=
| 4-x2 |
在同一坐标系中作图如下：
∵g（x）=mx+3m=m（x+3）为过定点（-3，0）的直线，
∴m=0时，显然g（x）=0与f（x）=
| 4-x2 |
当直线g（x）=mx+3m与曲线f（x）=
| 4-x2 |
| |3m| | ||
|
| 2 | ||
|
2
| ||
| 5 |
2
| ||
| 5 |
∴0≤m＜
2
| ||
| 5 |
2
| ||
| 5 |
故答案为：[0，
2
| ||
| 5 |
点评：本题考查根的存在性及根的个数判断，考查等价转化思想与数形结合思想的综合应用，属于中档题．
练习册系列答案
相关题目
如图所示的多面体中，DB⊥平面ABC，AE∥DB，且△ABE是边长为2的等边三角形，AE=1，BD=2．