题目内容
10.函数y=-$\frac{2}{x}$的单调增区间为( )| A. | [0,+∞) | B. | (-∞,0) | C. | (-∞,0),(0,+∞) | D. | (-∞,+∞) |
分析 利用反比例函数的单调性,可得反比例函数的单调增区间.
解答 解:函数的定义域为(-∞,0)∪(0,+∞),
函数y=-$\frac{2}{x}$的单调增区间为(-∞,0),(0,+∞),
故选C.
点评 本题考查了函数的单调性问题,求出函数的定义域,比较基础.

练习册系列答案
相关题目
5.已知直线l过抛物线y2=2px(p>0)的焦点F(1,0),交抛物线于M,N两点.
(Ⅰ)写出抛物线的标准方程及准线方程;
(Ⅱ)O为坐标原点,直线MO、NO分别交准线于点P,Q,求|PQ|的最小值.
(Ⅰ)写出抛物线的标准方程及准线方程;
(Ⅱ)O为坐标原点,直线MO、NO分别交准线于点P,Q,求|PQ|的最小值.
15.设复数z1=1+i,z2=1-bi,若z1•z2为纯虚数,则实数b=( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
2.下列函数中既是奇函数,又在区间(-1,1)上是增函数的为( )
| A. | y=|x+1| | B. | y=sinx | C. | y=2x+2-x | D. | y=lnx |
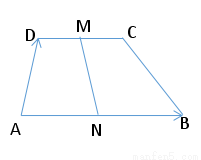
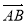 =a,
=a,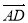 =b,试用a、b分别表示
=b,试用a、b分别表示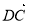 、
、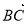 、
、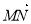 .
.
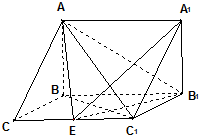 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=BB1=2,∠BCC1=$\frac{π}{3}$
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=BB1=2,∠BCC1=$\frac{π}{3}$