题目内容
15.设复数z1=1+i,z2=1-bi,若z1•z2为纯虚数,则实数b=( )| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
分析 直接利用复数代数形式的乘法运算化简z1•z2,然后由其实部等于0且虚部不等于0列式求解b的值.
解答 解:∵z1=1+i,z2=1-bi,
由z1•z2=(1+i)(1-bi)=(1+b)+(1-b)i为纯虚数,
得:$\left\{\begin{array}{l}{1+b=0}\\{1-b≠0}\end{array}\right.$,解得:b=-1.
故选:D.
点评 本题考查了复数代数形式的乘法运算,考查了复数的基本概念,是基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
10.函数y=-$\frac{2}{x}$的单调增区间为( )
| A. | [0,+∞) | B. | (-∞,0) | C. | (-∞,0),(0,+∞) | D. | (-∞,+∞) |
20. 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
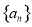 的前
的前 项和为
项和为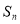 ,且
,且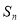
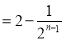 ,
,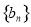 为等差数列,且
为等差数列,且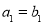 ,
,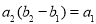 .
.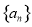 和
和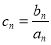 ,求数列
,求数列 的前
的前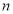 项和
项和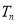 .
.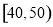 ,
,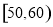 ,…,
,…,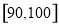 后得到如下频率分布直方图.
后得到如下频率分布直方图.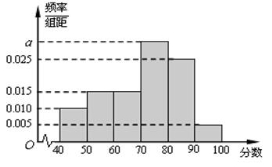
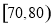 内的频率;
内的频率;