题目内容
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=-x2+2x,求函数f(x)的解析式.
考点:函数解析式的求解及常用方法,函数奇偶性的性质
专题:函数的性质及应用
分析:先求f(0)=0,再设x<0,由奇函数的性质f(x)=-f(-x),利用x>0时的表达式求出x<0时函数的表达式.
解答:
解:∵函数f(x)是定义在R上的奇函数,
∴f(0)=0,且f(-x)=-f(x),
∴f(x)=-f(-x),
设x<0,则-x>0,
∴f(-x)=-x2-2x,
∴f(x)=-f(-x)=-(-x2-2x)=x2+2x,
∴f(x)=
∴f(0)=0,且f(-x)=-f(x),
∴f(x)=-f(-x),
设x<0,则-x>0,
∴f(-x)=-x2-2x,
∴f(x)=-f(-x)=-(-x2-2x)=x2+2x,
∴f(x)=
|
点评:本题主要考查奇函数的性质求解函数的解析式,关键是利用原点两侧的函数表达式之间的关系解题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
下列函数中是偶函数且在(0,+∞)上单调递增的是( )
| A、y=2-x |
| B、y=lnx |
| C、y=x-2 |
| D、y=|x|-1 |
已知{an}是等比数列,(a6+a10)(a4+a8)=49,则a5+a9等于( )
| A、7 | B、±7 | C、14 | D、不确定 |
下列有关命题的说法中,错误的是( )
| A、若“p或q”为假命题,则p,q均为假命题 | ||||
| B、“x=1”是“x≥1”的充分不必要条件 | ||||
C、“x=
| ||||
| D、若命题p:”?实数x0,使x02≥0”则命题?p:“对于?x∈R,都有x2<0” |
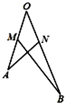 如图,M、N分别是线段OA、OB上的点,OM=MA=ON=1,NB=2,设
如图,M、N分别是线段OA、OB上的点,OM=MA=ON=1,NB=2,设