题目内容

已知{an}是等比数列，（a6+a10）（a4+a8）=49，则a5+a9等于（　　）
A、7B、±7C、14D、不确定
考点：等比数列的性质
专题：等差数列与等比数列
分析：设等比数列{an}的公比为q，利用等比数列的通项公式用“a5+a9”表示：（a6+a10）（a4+a8）=49，再求值即可．
解答： 解：设等比数列{an}的公比为q，且q≠0，
∵（a6+a10）（a4+a8）=49，
∴（a5•q+a9•q）（a5•
1
q
+a9•
1
q
）=49，
解得(a2+a9)2=49，
则a5+a9=±7，
故选：B．
点评：本题考查等比数列的通项公式的灵活应用，以及整体代换思想，属于基础题．
练习册系列答案
相关题目
在2014年巴西世界杯足球赛前夕，某体育用品店购进一批单价为40元的球服，如果按单价60元销售，那么一个月内可售出240套，根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高5元，销售量相应减少20套，设销售单价为x（x≥60）元，销售量为y套．
（1）求出y与x的函数关系式；
（2）当销售单价为多少元时，且销售额为14000元？
（3）当销售单价为多少元时，才能在一个月内获得最大利润，最大利润是多少？
已知函数f（x）是定义在R上的奇函数，当x＞0时，f（x）=-x2+2x，求函数f（x）的解析式．
函数f（x）=xex的导函数f′（x）等于（　　）
A、（1+x）ex
B、xex
C、ex
D、2xex
已知函数y=cos(ωx-
π
2
)(ω＞0)在区间[0，1]内至少出现2次极值，则ω的最小值为（　　）
A、
π
2
B、
3
2
π
C、
2
3
π
D、
5
6
π
已知函数f（x）=ex+e-x，其中e为自然对数的底数．
（1）若?x∈（0，+∞），mf（x）≤e-x+m-1，求实数m的取值范围；
（2）已知正数a满足：?x∈[1，+∞），f（x0）＜a（-x03+3x0）．试比较ea-1与ae-1大小，并证明你的结论．
复数（a2-a-2）+（|a-1|-1）i（a∈R）不是纯虚数，则有（　　）
A、a≠0B、a≠2
C、a≠0且a≠2D、a≠-1
已知等式|x-2|＞1的解集与关于x的不等式x2-ax+b＞0的解集相等．
（I）求实数a，b的值；
（Ⅱ）求函数f（x）=a
x-3
+b
4-x
的最大值．
已知f（x）=Asin（ωx+φ）（A＞0，ω＞0）的一段图象如下，则f（x）的解析式为（　　）
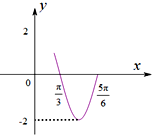
A、f(x)=2sin(2x+
4π
3
)
B、f(x)=2sin(2x-
π
3
)
C、f(x)=2sin(2x+
π
3
)
D、f(x)=2sin(2x-
π
6
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网