题目内容
已知函数f(x)=
lnx(x≥1),若将其图象绕点(1,0)逆时针旋转θ(θ∈(0,
))角后,所得图象仍是某函数的图象,则当角θ取最大值θ0时,tanθ0= .
| 3 |
| π |
| 2 |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:若函数f(x)逆时针旋转角θ后所得曲线仍是一函数,根据函数的定义中的“唯一性”可得函数f(x)的图象应满足:一个自变量对应一个函数值y,因此,画出函数的图象,找切线的临界位置.
解答:
解:画出函数图象,如图:
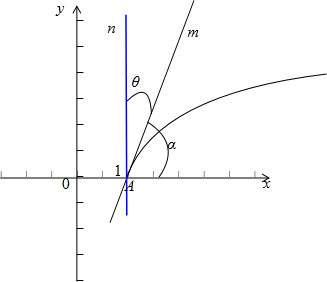
易知函数图象过A(1,0)
A(1,0)处的切线m转动到直线n的位置(也即和x轴垂直)时就是转动的最大角度,此后若再旋转,图象的一个x值将对应2个y,那样就不是函数的图象了.因此只要求出初始位置时切线和终了位置时的切线的夹角θ即为转动的最大角度θ0.
设切线m的倾斜角为α,∴tanα=f′(1),
∵f′(x)=
,∴tanα=f′(1)=
,∴α=
,∴θ=
,∴θ0=
∴tan
=
故答案为:

易知函数图象过A(1,0)
A(1,0)处的切线m转动到直线n的位置(也即和x轴垂直)时就是转动的最大角度,此后若再旋转,图象的一个x值将对应2个y,那样就不是函数的图象了.因此只要求出初始位置时切线和终了位置时的切线的夹角θ即为转动的最大角度θ0.
设切线m的倾斜角为α,∴tanα=f′(1),
∵f′(x)=
| ||
| x |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
∴tan
| π |
| 6 |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查的知识点是函数的定义,其中根据函数的定义分析出函数f(x)的图象满足一个自变量对应一个函数值y是解答本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知数列{an}前n项和Sn=n2-n,正项等比数列{bn}中,b2=a3,bn+3bn-1=4bn2(n≥2,n∈N+),则bn=( )
| A、2n-1 |
| B、2n |
| C、2n-2 |
| D、22n-1 |
已知函数y=cos(ωx-
)(ω>0)在区间[0,1]内至少出现2次极值,则ω的最小值为( )
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|