题目内容

函数f（x）=lg（3x-1）的定义域为（　　）
A、(
1
3
，+∞)
B、(-∞，
1
3
)
C、[
1
3
，+∞)
D、（0，+∞）
考点：对数函数的定义域,函数的定义域及其求法
专题：函数的性质及应用
分析：利用对数函数的定义域即可得出．
解答： 解：要使函数f（x）=lg（3x-1）有意义，
必须满足3x-1＞0，解得x＞
1
3
．
故函数f（x）的定义域为(
1
3
，+∞)．
故选：A．
点评：本题考查了对数函数的定义域，属于基础题．
练习册系列答案
相关题目
分别从集合A={1，2，3，4}和集合B={5，6，7，8}中各取一个数，则这两数之积为偶数的概率是
 
．
324与135的最大公约数为
 
．
已知函数f（x）=
2x+1，x＜1
x2+ax，x≥1
，若f[f（0）]=4a，则
∫
2
1
a
x
dx=（　　）
A、2ln2
B、
1
3
ln2
C、ln2
D、9ln2
已知集合A={x|0＜x＜2}，B={x|（x-1）（x+1）＞0}，则A∪B=（　　）
A、（0，1）
B、（1，2）
C、（-∞，-1）∪（0，+∞）
D、（-∞，-1）∪（1，+∞）
已知平面内一动点P到点F（0，1）的距离与点P到y=-1的距离相等．
（Ⅰ）求动点P的轨迹方程C；
（II）过点F作两条斜率存在且互相垂直的直线L1，L2，设L1与轨迹C相交于点A，B，L2与轨迹C相交于点D，E，当
AD
•
.
EB
的取到最小值时，求L1直线的方程．
在平面直角坐标系xOy中，点A（0，27
3
 ）在y轴正半轴上，点Pn（3n-1，0）在x轴上，记∠PnAPn+1=θn，yn=tanθn，n∈N*，则yn 取最大值时，θn的值为
 
．
函数y=x（x2-1）的大致图象是（　　）
A、
B、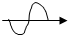
C、
D、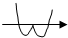
已知等比数列{an}的公比q=
1
2
，其前4项和S4=60，则a2等于（　　）
A、8B、12C、16D、20

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网