题目内容
11.以极点为原点,极轴为x轴的正半轴,单位长度一致建立平面直角坐标系,曲线C:$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),直线l:极坐标方程为ρsin(θ-$\frac{π}{3}$)=1.(Ⅰ)求曲线C的普通方程,直线l的直角坐标方程;
(Ⅱ)求曲线C上的点到直线l的距离的最大值.
分析 (Ⅰ) 曲线C:$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),利用平方关系可得曲线C的普通方程.直线l:极坐标方程为ρsin(θ-$\frac{π}{3}$)=1,展开为:ρsinθ-$\sqrt{3}$ρcosθ=2,利用互化公式可得直角坐标方程.
(Ⅱ) 利用点到直线的距离公式可得:圆心C(0,0)到直线的距离d,因此所求的最大值=d+r.
解答 解:(Ⅰ) 曲线C:$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),利用平方关系可得:曲线C:x2+y2=1.
直线l:极坐标方程为ρsin(θ-$\frac{π}{3}$)=1,展开为:ρsinθ-$\sqrt{3}$ρcosθ=2,可得直角坐标方程:$\sqrt{3}$x-y+2=0.
(Ⅱ) 圆心C(0,0)到直线的距离d=$\frac{|0-0+2|}{\sqrt{(\sqrt{3})^{2}+{1}^{2}}}$,因此所求的最大值=d+r=1+1=2.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.若$\overrightarrow a=(1,2)$,$\overrightarrow b=(m,1)$,若$\overrightarrow a⊥\overrightarrow b$,则m=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
19.全集U={1,2,3,4,5},集合A={1,2},集合B={1,3,5},则图中阴影部分所表示的集合是( )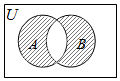

| A. | {1} | B. | {1,2,3,5} | C. | { 2,3,5} | D. | {4} |
6.已知△ABC中内角A为钝角,则复数(sinA-sinB)+i(sinB-cosC)对应点在( )
| A. | 第Ⅰ象限 | B. | 第Ⅱ象限 | C. | 第Ⅲ象限 | D. | 第Ⅳ象限 |
3.数列{an}的通项公式为an=3n-23,当Sn取到最小时,n=( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
1.对于在R上可导的任意函数f(x),若其导函数为f′(x),且满足(x-1)f′(x)≥0,则必有( )
| A. | f(0)+f(2)≤2f(1) | B. | f(0)+f(2)<2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |