题目内容
6.已知△ABC中内角A为钝角,则复数(sinA-sinB)+i(sinB-cosC)对应点在( )| A. | 第Ⅰ象限 | B. | 第Ⅱ象限 | C. | 第Ⅲ象限 | D. | 第Ⅳ象限 |
分析 ①△ABC中内角A为钝角,可得A>B,A=π-(B+C),∴sinA-sinB=sin(B+C)-sinB,根据A为钝角,可得0<B<B+C<$\frac{π}{2}$,利用正弦函数的单调性即可得出sinA-sinB>0.
②由0<B+C<$\frac{π}{2}$,可得0<B<$\frac{π}{2}$-C$<\frac{π}{2}$,可得sinB<sin($\frac{π}{2}$-C)=cosC.即可复数(sinA-sinB)+i(sinB-cosC)对应点(sinA-sinB,sinB-cosC)在第四象限.
解答 解:①∵△ABC中内角A为钝角,∴A>B,A=π-(B+C),
∴sinA-sinB=sin[π-(B+C)]-sinB=sin(B+C)-sinB,
∵A为钝角,∴0<B<B+C<$\frac{π}{2}$,
∴sin(B+C)>sinB,即sin(B+C)-sinB>0,
则sinA-sinB>0.
②∵0<B+C<$\frac{π}{2}$,∴0<B<$\frac{π}{2}$-C$<\frac{π}{2}$,∴sinB<sin($\frac{π}{2}$-C)=cosC,
∴sinB<cosC,
∴复数(sinA-sinB)+i(sinB-cosC)对应点(sinA-sinB,sinB-cosC)在第四象限.
故选:D.
点评 本题考查了三角函数的单调性求值诱导公式、三角形内角和定理、复数的几何意义,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设α是第二象限角,cosα=-$\frac{3}{5}$,则tanα=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
1.命题:?x∈Z,x2∈Z的否定是命题( )
| A. | ?x∈Z,x2∉Z | B. | ?x∉Z,x2∉Z | C. | ?x∈Z,x2∈Z | D. | ?x∈Z,x2∉Z |
15.已知函数f(x)=ax-1+4的图象恒过定点P,则点P的坐标是( )
| A. | (1,5) | B. | (1,4) | C. | (0,4) | D. | (4,0) |
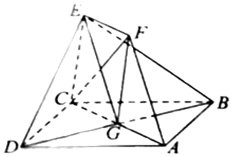 (理)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(理)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.