题目内容
经过计算:1,1+2+1,1+2+3+2+1,1+2+3+4+3+2+1的值,可以猜测等式1+2+3+…+(n-1)+n+(n-1)+…+3+2+1= .
考点:归纳推理
专题:推理和证明
分析:由已知中1=12,1+2+1=4=22,1+2+3+2+1=9=32,1+2+3+4+3+2+1=16=42,…归纳猜想可得:1+2+3+…+(n-1)+n+(n-1)+…+3+2+1=n2,进而可得答案.
解答:
解:由已知中:
1=12,
1+2+1=4=22,
1+2+3+2+1=9=32,
1+2+3+4+3+2+1=16=42,
…
归纳猜想可得:1+2+3+…+(n-1)+n+(n-1)+…+3+2+1=n2,
故答案为:n2
1=12,
1+2+1=4=22,
1+2+3+2+1=9=32,
1+2+3+4+3+2+1=16=42,
…
归纳猜想可得:1+2+3+…+(n-1)+n+(n-1)+…+3+2+1=n2,
故答案为:n2
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线y=kx+3与圆(x-2)2+(y-3)2=4相交于M、N两点,若|MN|≥2
,则直线倾斜角的取值范围是( )
| 3 |
A、[
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[
|
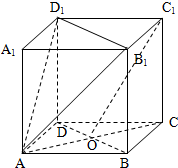 已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点,
已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点,