题目内容
19.在(tanx+cotx)10的二项展开式中,tan2x的系数为210(用数值作答)分析 通项公式Tr+1=${∁}_{10}^{r}$tan10-rx•cotrx=${∁}_{10}^{r}$tan10-2rx,令10-2r=2,解得r即可得出.
解答 解:通项公式Tr+1=${∁}_{10}^{r}$tan10-rx•cotrx=${∁}_{10}^{r}$tan10-2rx,
令10-2r=2,解得r=4.
∴tan2x的系数=${∁}_{10}^{4}$=210.
故答案为:210.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.若函数f(x)=x2-4x+a对于一切x∈[0,1]时,恒有f(x)≥0成立,则实数a的取值范围是( )
| A. | [3,+∞) | B. | (3,+∞) | C. | (-∞,3] | D. | (-∞,3) |
4.如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是( )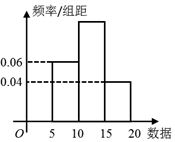

| A. | 12.5 11 | B. | 12.5 12 | C. | 12.5 13 | D. | 12.5 14 |
11.化简$\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{BD}-\overrightarrow{CD}$=( )
| A. | 0 | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{DA}$ | D. | $\overrightarrow 0$ |
8.若a为实数,i为虚数单位,且$\frac{2+ai}{1+i}=3+i$,则a=( )
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
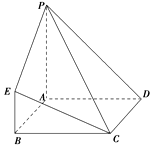 在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.