题目内容
17.已知函数f(x)是R上的偶函数,满足f(x)=-f(x+1),当x∈[2015,2016]时,f(x)=x-2017,则( )| A. | $f(sin\frac{π}{3})>f(cos\frac{π}{3})$ | B. | f(sin2)>f(cos2) | C. | $f(sin\frac{π}{5})<f(cos\frac{π}{5})$ | D. | f(sin1)<f(cos1) |
分析 求出函数以2为周期,f(x)=-x-1(x∈[0,1]),利用函数的单调性,即可得出结论.
解答 解:∵f(x)=-f(x+1),
∴f(x+2)=f(x),即函数以2为周期,
设x∈[-1,0],∴x+2016∈[2015,2016],
∵当x∈[2015,2016]时,f(x)=x-2017,
∴f(x)=f(x+2016)=x-1,
设x∈[0,1],则-x∈[-1,0],∴f(-x)=-x-1,
∵函数f(x)是R上的偶函数,
∴f(x)=-x-1(x∈[0,1]),
∵sin1>cos1,
∴f(sin1)<f(cos1),
故选D.
点评 本题考查函数的单调性与周期性,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若a为实数,i为虚数单位,且$\frac{2+ai}{1+i}=3+i$,则a=( )
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
2.下列函数中是奇函数,且最小正周期是π的函数是( )
| A. | $y=cos({\frac{3π}{2}-2x})$ | B. | y=|cosx| | C. | $y=sin({\frac{π}{2}+2x})$ | D. | y=|sinx| |
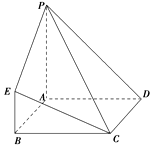 在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.