设实数x.y满足$\left\{\begin{array}{l}{2x+y≥4}\\{x-y≥-1}\\{x-2y≤2}\end{array}\right.$.则z=x+y为( )A．有最小值2.无最大值B．有最小值2.最大值3C．有最大值3.无最小值D．既无最小值.也无最大值题目和参考答案——青夏教育精英家教网—

题目内容

6．设实数x、y满足$\left\{\begin{array}{l}{2x+y≥4}\\{x-y≥-1}\\{x-2y≤2}\end{array}\right.$，则z=x+y为（　　）

	A．	有最小值2，无最大值		B．	有最小值2，最大值3
	C．	有最大值3，无最小值		D．	既无最小值，也无最大值

分析先根据约束条件画出可行域，再利用几何意义求最值，只需求出直线z=x+y过点A时，z的最小值即可．

解答解：先根据约束条件$\left\{\begin{array}{l}{2x+y≥4}\\{x-y≥-1}\\{x-2y≤2}\end{array}\right.$画出可行域，
由图知，当直线z=x+y过点A（2，0）时，z最小值为：2．
当直线z=x+y没有最大值．
故选：A．

点评本题主要考查了简单的线性规划，以及利用几何意义求最值，属于中档题．

练习册系列答案

17．i为虚数单位，若$\frac{a+bi}{i}$（a，b∈R）与（2-i）²互为共轭复数，则a-b=（　　）

14．已知{a_n}是各项均为正数的等比数列，a₁₁=8，设b_n=log₂a_n，且b₄=17．
（Ⅰ）求证：数列{b_n}是以-2为公差的等差数列；
（Ⅱ）设数列{b_n}的前n项和为S_n，求S_n的最大值．

1．设变量x、y满足约束条件$\left\{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}\right.$，则目标函数z=x²+y²的最大值为（　　）

2．|$\overrightarrow{a}$|=10，|$\overrightarrow{b}$|=36，$\overrightarrow{a}$•$\overrightarrow{b}$=-180，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是$\frac{2π}{3}$．

9．已知集合M={x|x²-3x＜0}，N={x|1≤x≤4}，则M∩N=（　　）

6．设向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|=3，则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=4$\sqrt{2}$．

7．

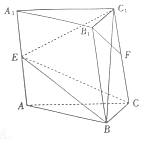如图，已知直三棱柱ABC-A₁B₁C₁的底面是边长为4的正三角形，B，E，F分别是AA₁，CC₁的中点，且BE⊥B₁F．
（1）求证：B₁F⊥EC₁；
（2）求二面角C₁-BE-C的余弦值．

试题分类