题目内容

8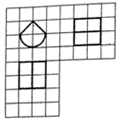．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中曲线部分是圆弧，则此几何体的表面积为（　　）
A．2+4$\sqrt{2}$+3πB．2+4$\sqrt{2}$+5πC．10+πD．20+2π

分析 由题意，几何体的直观图是半圆柱与三棱柱的组合体，即可求出几何体的表面积．

解答 解：由题意，几何体的直观图是半圆柱与三棱柱的组合体，几何体的表面积为
π+$π•1•2+2•\frac{1}{2}•1•2$+2$•2•\sqrt{2}$=2+4$\sqrt{2}$+3π，
故选A．

点评 本题考查由三视图求几何体的表面积，确定几何体的形状是关键．

练习册系列答案
相关题目
18．已知$f（x）=\left\{\begin{array}{l}2a-（x+\frac{4}{x}），x＜a\\ x-\frac{4}{x}，x≥a\end{array}\right.$．
①当a=1时，f（x）=3，则x=4；
②当a≤-1时，若f（x）=3有三个不等实数根，且它们成等差数列，则a=$-\frac{11}{6}$．
19．已知集合A={3a，3}，B={a2+2a，4}，A∩B={3}，则A∪B等于（　　）
A．{3，5}B．{3，4}C．{-9，3}D．{-9，3，4}
16．已知函数f（x）=（x2+x-1）ex，则曲线y=f（x）在点（1，f（1））处的切线方程为（　　）
A．y=3ex-2eB．y=3ex-4eC．y=4ex-5eD．y=4ex-3e
3．设复数z=$\frac{1+i}{1-i}$，则z$\overline{z}$=（　　）
A．1+iB．1-iC．1D．2
13．在△ABC中，∠BAC=90°，AB=3，AC=4，若点D、E都在边BC上，且∠BAD=∠CAE=15°，则$\frac{BD•BE}{CD•CE}$=$\frac{9}{16}$．
20．已知复数z=$\frac{2-i}{1+i}$（其中i为虚数单位），则|z|=（　　）
A．$\frac{\sqrt{5}}{2}$B．$\frac{\sqrt{10}}{2}$C．$\frac{3\sqrt{2}}{2}$D．$\sqrt{10}$
17．i为虚数单位，若$\frac{a+bi}{i}$（a，b∈R）与（2-i）2互为共轭复数，则a-b=（　　）
A．1B．-1C．7D．-7
9．已知集合M={x|x2-3x＜0}，N={x|1≤x≤4}，则M∩N=（　　）
A．[1，3）B．（1，3）C．（0，3]D．（-∞，-5]∪[6，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网