题目内容
8.下列函数中,在其定义域内,既是奇函数又是减函数的是( )| A. | f(x)=x3 | B. | f(x)=$\sqrt{-x}$ | C. | f(x)=2-x-2x | D. | f(x)=-lg|x| |
分析 根据题意,对选项中的函数的奇偶性与单调性进行判断分析即可.
解答 解:对于A,f(x)=x3,在定义域R内,是奇函数,也是增函数,不满足题意;
对于B,f(x)=$\sqrt{-x}$,定义域是(-∞,0],非奇非偶的函数,不满足题意;
对于C,f(x)=2-x-2x,定义域是R,且f(-x)=2x-2-x=-(2-x-2x)=-f(x),是奇函数;
也是定义域上的减函数,满足题意;
对于D,f(x)=-lg|x|,是定义域上的偶函数,不满足题意.
故选:C.
点评 本题考查了基本初等函数的奇偶性与单调性的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知复数z=2+i,则$\frac{\overline{z}}{z}$=( )
| A. | $\frac{3}{5}$-$\frac{4}{5}$i | B. | -$\frac{3}{5}$+$\frac{4}{5}$i | C. | $\frac{5}{3}$-$\frac{4}{3}$i | D. | -$\frac{5}{3}$+$\frac{4}{3}$i |
17.已知集合A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=2x,x∈A},则A∩B=( )
| A. | [0,1) | B. | [1,2] | C. | (2,4] | D. | [2.4] |
14.设a∈R,若复数z=$\frac{a-i}{3+i}$(i是虚数单位)的实部为2,则a的值为( )
| A. | 7 | B. | -7 | C. | 5 | D. | -5 |
18.一个物体的运动方程为s=1-t+t2,其中s的单位是米,t的单位是秒,那么物体在3秒这个时刻的瞬时速度是( )
| A. | 7米/秒 | B. | 6米/秒 | C. | 5米/秒 | D. | 8米/秒 |
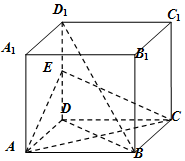 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为DD1中点,
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为DD1中点,