题目内容
3．已知x，2x+2，3x+3是一个等比数列的前三项，则公比q=$\frac{3}{2}$．分析 由题意列式求得x值，代入即可求得公比．
解答 解：由题意，（2x+2）2=x（3x+3），即x2+5x+4=0，解得x=-1或x=-4．
当x=-1时，2x+2=0，不合题意；
当x=-4时，三个数为-4，-6，-9．
公比为：$\frac{3}{2}$．
故答案为：$\frac{3}{2}$．
点评 本题考查等比数列的通项公式，考查了等比数列的性质，是基础题．
练习册系列答案
相关题目
11．已知双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，|F1F2|=6，P是E右支上一点，PF1与y轴交于点A，△PAF2的内切圆在边AF2上的切点为Q，若|AQ|=$\sqrt{3}$，则E的离心率是（ ）
| A． | 2$\sqrt{3}$ | B． | $\sqrt{5}$ | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
9．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{a}（2-x），x≤1}\\{|x-5|-1，3≤x≤7}\end{array}\right.$（a＞0，且a≠1）的图象上关于直线x=1对称的点有且仅有一对，则实数a的取值范围是（ ）
| A． | [$\frac{1}{7}$，$\frac{1}{5}$]∪{3} | B． | [3，5]∪{$\frac{1}{7}$} | C． | [$\frac{1}{7}$，$\frac{1}{3}$）∪{5} | D． | [3，7）∪{$\frac{1}{5}$} |
8．下列函数中，在其定义域内，既是奇函数又是减函数的是（ ）
| A． | f（x）=x3 | B． | f（x）=$\sqrt{-x}$ | C． | f（x）=2-x-2x | D． | f（x）=-lg|x| |
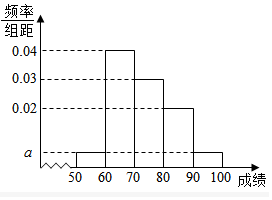某小学1000名学生期中考试数学成绩的频率分布直方图如图所示．其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．根据统计学的知识估计成绩在[80，90）内的人数约为200．