题目内容

15．已知角θ的顶点在坐标原点，始边为x轴的正半轴，若A（x，-1）是角θ终边上的一点，且cosθ=$\frac{2\sqrt{5}}{5}$，则x的值为（　　）
A．-2B．2C．-3D．3

分析 由任意角的三角函数的定义，通过cosθ=$\frac{x}{r}$=$\frac{x}{\sqrt{{x}^{2}+1}}$=$\frac{2\sqrt{5}}{5}$，由此解得x的值．

解答 解：由任意角的三角函数的定义可得cosθ=$\frac{x}{r}$=$\frac{x}{\sqrt{{x}^{2}+1}}$=$\frac{2\sqrt{5}}{5}$，
解得x=2．
故选：B．

点评 本题主要考查任意角的三角函数的定义，考查学生的计算能力，属于基础题．

练习册系列答案
相关题目
5．各棱长都等于4的四面ABCD中，设G为BC的中点，E为△ACD内的动点（含边界），且GE∥平面ABD，若$\overrightarrow{AE}$•$\overrightarrow{BD}$=1，则|$\overrightarrow{AE}$|=$\frac{\sqrt{21}}{2}$．
6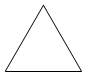．一个正三棱柱的侧棱长和底面边长相等，体积为$16\sqrt{3}c{m^3}$，它的三视图中的俯视图如图所示，侧视图是一个矩形，则侧视图的面积是（　　）
A．8B．$8\sqrt{3}$C．4D．$4\sqrt{3}$
3．已知函数f（x）在其定义区间[a，b]上满足①f（x）＞0；②f′（x）＜0；③对任意的x1，x2∈[a，b]，式子$f（{\frac{{{x_1}+{x_2}}}{2}}）$≤$\frac{{f（{x_1}）+f（{x_2}）}}{2}$恒成立．记S1=$\int_{\;\;a}^{\;\;b}$f（x）dx，S2=$\frac{f（a）+f（b）}{2}$•（b-a），S3=f（b）（b-a），则S1，S2，S3的大小关系为s3＜s1≤s2．（按由小到大的顺序）
10．设m=${∫}_{0}^{1}$exdx，n=${∫}_{1}^{e}$$\frac{1}{x}$dx，则m与n的大小关系为（　　）
A．m＜nB．m≤nC．m＞nD．m≥n
20．计算不定积分${∫}_{\;}^{\;}$$\frac{{x}^{3}+3{x}^{2}sinx+2x-1}{{x}^{2}}$dx．
7．若扇形的周长为16cm，圆心角为2rad，则该扇形的面积为16cm2．
4．化简：$\frac{1}{{sin{{10}°}}}$-$\frac{{\sqrt{3}}}{{cos{{10}°}}}$的结果是（　　）
A．1B．$\sqrt{3}$C．2D．4
5．在平面直角坐标系xOy中，已知A（cosα，sinα），B（cosβ，sinβ）是直线y=$\sqrt{3}$x+$\sqrt{2}$上的两点，则tan（α+β）的值为-$\sqrt{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网