题目内容
点A（3，2），B（-2，7），若y=ax-3与线段AB的交点P分有向线段AB的比为4：1，则a的值（ ）
| A、3 | B、-3 | C、9 | D、-9 |
考点：平面向量坐标表示的应用
专题：平面向量及应用
分析：利用定比分点求出分点坐标，代入直线方程求解即可．
解答：
解：y=ax-3与线段AB的交点P分有向线段AB的比为4：1，
设分点P（c，b），则
=4
，
即（c-3，b-2）=4（-2-c，7-b）
解得c=-1，b=6，
P（-1，6），代入直线方程y=ax-3可得：
a=-9．
故选：D．
设分点P（c，b），则
| AP |
| PB |
即（c-3，b-2）=4（-2-c，7-b）
解得c=-1，b=6，
P（-1，6），代入直线方程y=ax-3可得：
a=-9．
故选：D．
点评：本题考查向量在几何中的应用，定比分点坐标的求法，考查计算能力．
练习册系列答案
相关题目
已知在复平面内，复数z对应的点在第一象限，且满足z2+2
=2，则复数z的共轭复数
的虚部为（ ）
. |
| z |
. |
| z |
| A、1 | B、-i | C、-1 | D、i |
如图所示的流程图，若输出的结果是9，则判断框中的横线上可以填入的最大整数为（ ）
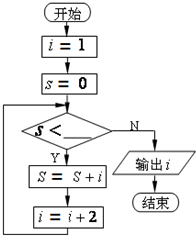
| A、17 | B、16 | C、15 | D、14 |
设k∈R，则“k≠1”是“直线l：y=kx+
与圆x2+y2=1不相切”的（ ）
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
如图，AE⊥平面DEC，四边形ABCD为正方形，M，N分别是线段BE、DE中点．