Question

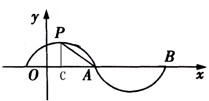已知函数f（x）=sin[ωπ（x+

1

3

）]的部分图象如图，其中P为函数图象的最高点，PC⊥x轴，且tan∠APC=1．
（1）求函数f（x）的解析式；
（2）若x∈[1，2]，求函数f（x）的取值范围．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的图象

专题：三角函数的图像与性质

分析：（1）由题意可得T=

2π

ω

=4AC=4，求得ω的值，可得函数的解析式．
（2）由x∈[1，2]，利用正弦函数的定义域和值域，求得函数f（x）的取值范围．

解答： 解：（1）由函数f（x）=sin[ωπ（x+

1

3

）]的部分图象，PC⊥x轴，且tan∠APC=1，可得T=

2π

ω

=4AC=4，∴ω=

1

2

，
故函数f（x）=sin[

1

2

π（x+

1

3

）=sin（

πx

2

+

π

6

）．
（2）若x∈[1，2]，则

πx

2

+

π

6

∈[

2π

3

，

7π

6

]，∴sin（

πx

2

+

π

6

）∈[-

1

2

，

3

2

]．

点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，正弦函数的定义域和值域，属于基础题．