题目内容
复数z=
的共轭复数为（ ）
| 5-2i |
| i |
| A、-5i+2 | B、5i-2 |
| C、-5i-2 | D、5i+2 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用复数的运算法则、共轭复数的定义即可得出．
解答：
解：z=
=
=-5i-2的共轭复数为5i-2．
故选；B．
| 5-2i |
| i |
| -i(5-2i) |
| -i•i |
故选；B．
点评：本题考查了复数的运算法则、共轭复数的定义，属于基础题．
练习册系列答案
名题金卷系列答案
相关题目
已知命题p：椭圆、双曲线、抛物线和圆统称为圆锥曲线．命题q：微积分是由牛顿和莱布尼茨于17世纪中叶创立的．则以下命题中为真命题的一个是（ ）
| A、p∨q |
| B、（￢p）∧q |
| C、p∧（￢q） |
| D、（￢p）∨（￢q） |
随机变量X的概率分布规律为P（X=n）=
（n=1，2，3），其中a是常数，则P（1≤X≤2）的值为（ ）
| a |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中，正确的命题的个数是（ ）
a．若角α在第二象限，且sinα=m，cosα=n，则tanα=-
b．无论α为何角，都有sin2α+cos2α=1
c．总存在一个角α，使得sinα+cosα=1
d．总存在一个角α，使得sinα=cosα=
．
a．若角α在第二象限，且sinα=m，cosα=n，则tanα=-
| m |
| n |
b．无论α为何角，都有sin2α+cos2α=1
c．总存在一个角α，使得sinα+cosα=1
d．总存在一个角α，使得sinα=cosα=
| 1 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
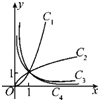图中的曲线是幂函数y=xn在第一象限的图象，已知n可取±2，±| 1 |
| 2 |
A、-2，-
| ||||
B、2，
| ||||
C、-
| ||||
D、2，
|
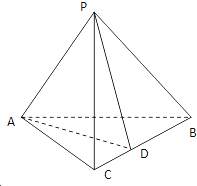如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC，点D为BC中点．