题目内容
设f(x)=ax5+bx+2,(ab≠0),若f(3)=9,则f(-3)= .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:法1:根据条件求出a•35+3b=7,利用整体代换即可得到结论.
法2:构造函数f(x)-2=ax5+bx,判断函数的奇偶性,即可得到结论.
法2:构造函数f(x)-2=ax5+bx,判断函数的奇偶性,即可得到结论.
解答:
解:法1:∵f(x)=ax5+bx+2,(ab≠0),
∴若f(3)=9,则f(3)=a•35+3b+2=9,
即a•35+3b=7,
则f(-3)=-a•35-3b+2=-(a•35+3b)+2=-7+2=-5.
法2:由f(x)=ax5+bx+2,
得f(x)-2=ax5+bx,
设g(x)=f(x)-2=ax5+bx,
则g(-x)=-g(x),则g(x)是奇函数,
则g(-2)=-g(2),
即f(-2)-2=-[f(2)-2]=-(9-2)=-7,
则f(-2)=2-7=-5.
故答案为:-5
∴若f(3)=9,则f(3)=a•35+3b+2=9,
即a•35+3b=7,
则f(-3)=-a•35-3b+2=-(a•35+3b)+2=-7+2=-5.
法2:由f(x)=ax5+bx+2,
得f(x)-2=ax5+bx,
设g(x)=f(x)-2=ax5+bx,
则g(-x)=-g(x),则g(x)是奇函数,
则g(-2)=-g(2),
即f(-2)-2=-[f(2)-2]=-(9-2)=-7,
则f(-2)=2-7=-5.
故答案为:-5
点评:本题主要考查函数值的计算,根据条件利用整体代换是解决本题的关键.利用构造f(x)-2=ax5+bx,利用函数的奇偶性也可.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
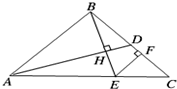 等腰直角△ABC中,AD是直角边BC上的中线,BE⊥AD,交AC于E,EF⊥BC,若AB=BC=a,则EF等于( )
等腰直角△ABC中,AD是直角边BC上的中线,BE⊥AD,交AC于E,EF⊥BC,若AB=BC=a,则EF等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知a,b,c依次为函数f(x)=2x+x,g(x)=log2x-1,h(x)=2x-log
x的零点,则a,b,c的大小关系为( )
| 1 |
| 2 |
| A、a<b<c |
| B、a<c<b |
| C、c<a<b |
| D、b<a<c |
若抛物线y2=ax(a>0)上存在两点M,N关于直线y=x-2对称,则a的取值范围是( )
A、0<a<
| ||
B、0<a<
| ||
| C、0<a<2 | ||
D、0<a<
|
在复平面内,复数z=
-
对应的点位于( )
| 1 |
| 2 |
| i |
| 2 |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |