题目内容
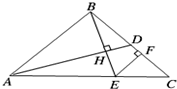 等腰直角△ABC中,AD是直角边BC上的中线,BE⊥AD,交AC于E,EF⊥BC,若AB=BC=a,则EF等于( )
等腰直角△ABC中,AD是直角边BC上的中线,BE⊥AD,交AC于E,EF⊥BC,若AB=BC=a,则EF等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:平面向量的基本定理及其意义
专题:立体几何
分析:如图所示,设∠BAD=α,根据等腰直角△ABC中,AD是直角边BC上的中线,可得tanα=
=
.又∠DBH=90°-∠BDA=α.可得:EF=BFtanα=
BF.由已知可得EF=FC.根据FC+BF=EF+2EF=a,即可得出.
| BD |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:如图所示,
设∠BAD=α,
∵等腰直角△ABC中,AD是直角边BC上的中线,
∴tanα=
=
.
∵BE⊥AD,
∴∠DBH=90°-∠BDA=α.
在Rt△BEF中,EF=BFtanα=
BF.
在Rt△EFC中,∠C=45°,∴EF=FC.
∴FC+BF=EF+2EF=a,
解得EF=
a.
故选:C.

设∠BAD=α,
∵等腰直角△ABC中,AD是直角边BC上的中线,
∴tanα=
| BD |
| AB |
| 1 |
| 2 |
∵BE⊥AD,
∴∠DBH=90°-∠BDA=α.
在Rt△BEF中,EF=BFtanα=
| 1 |
| 2 |
在Rt△EFC中,∠C=45°,∴EF=FC.
∴FC+BF=EF+2EF=a,
解得EF=
| 1 |
| 3 |
故选:C.
点评:本题考查了直角三角形的边角关系、等腰直角三角形的性质,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
已知a>0,b>0,f=
,则f的最小值为( )
| (a+4b)(ab+4) |
| ab |
| A、8 | B、16 | C、20 | D、25 |
已知sin(
-x)=
,且
<x<
,则sin2x的值为( )
| π |
| 4 |
| 3 |
| 5 |
| 17π |
| 12 |
| 7π |
| 4 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知函数f(x)=
,g(x)=2x.若函数y=f(x)-g(x)恰有3个零点,则实a的值是( )
|
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
执行如图所示的程序框图,会输出一列数,则这个数列的第3项是( )


| A、870 | B、30 | C、6 | D、3 |
 已知矩形ABCD,P为平面ABCD外一点,M、N分别为BC、PD的中点,且满足
已知矩形ABCD,P为平面ABCD外一点,M、N分别为BC、PD的中点,且满足