题目内容
 如图,△ABC的三个内角分别为A,B,C,cosA=
如图,△ABC的三个内角分别为A,B,C,cosA=| 1 |
| 3 |
2
| ||
| 3 |
(1)求角C的大小;
(2)当CD=8
| 2 |
考点:余弦定理,正弦定理
专题:三角函数的求值,解三角形
分析:(1)依题意,可求得cos2A+cos2B=1,于是可得sinA=cosB,即A、B互余,从而得角C的大小;
(2)当CD=8
-4时,利用正弦定理可求得AD=
=6
-3,BD=
=24-6
,从而可求AC,BC的长.
(2)当CD=8
| 2 |
| CDsin∠ACD |
| sinA |
| 2 |
| CD×sin∠BCD |
| sinB |
| 2 |
解答:
解:(1)∵cosA>0,cosB>0,且A,B是,△ABC的内角,
∴0<A<
,0<B<
,
又cos2A+cos2B=
+
=1,
∴sin2A=cos2B,sinA=cosB=sin(
-B),
∴A+B=
,故C=
.
(2)由(1)知,C=
,∴∠DCB=
,
又sinA=cosB=
,sinB=cosA=
,
在△ABC中,由正弦定理得:AD=
=
=6
-3,
在△ABC中,由正弦定理得:BD=
=
=24-6
,
∴AB=AD+BD=6
-3+24-6
=21,
∴AC=ABsinB=21×
=7,
DC=AB×sinA=21×
=14
.
∴0<A<
| π |
| 2 |
| π |
| 2 |
又cos2A+cos2B=
| 1 |
| 9 |
| 8 |
| 9 |
∴sin2A=cos2B,sinA=cosB=sin(
| π |
| 2 |
∴A+B=
| π |
| 2 |
| π |
| 2 |
(2)由(1)知,C=
| π |
| 2 |
| π |
| 4 |
又sinA=cosB=
2
| ||
| 3 |
| 1 |
| 3 |
在△ABC中,由正弦定理得:AD=
| CDsin∠ACD |
| sinA |
(8
| ||||||
|
| 2 |
在△ABC中,由正弦定理得:BD=
| CD×sin∠BCD |
| sinB |
(8
| ||||||
|
| 2 |
∴AB=AD+BD=6
| 2 |
| 2 |
∴AC=ABsinB=21×
| 1 |
| 3 |
DC=AB×sinA=21×
2
| ||
| 3 |
| 2 |
点评:本题考查同角三角函数间的关系,着重考查正弦定理与余弦定理的综合运用,考查推理、运算与求解能力,属于中档题.

练习册系列答案
相关题目
从8名学生中,男生选2人,女生选1人,分别参加语、数、英三科比赛,共有90种不同方案,那么男、女生人数是( )
| A、2男6女 | B、6男2女 |
| C、5男3女 | D、3男5女 |
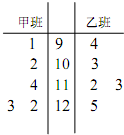 为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图:
为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图: