题目内容
已知函数f(x)=(mx+n)e-x(m,n∈R,e为自然数)
①若函数f(x)在点(1,f(1))处的切线方程为x+ey-3=0,试确定函数f(x)的单调区间.
②当n=-1,m∈R时,若对于任意x∈[
,1]都有f(x)≥x恒成立,求实数m的最小值.
①若函数f(x)在点(1,f(1))处的切线方程为x+ey-3=0,试确定函数f(x)的单调区间.
②当n=-1,m∈R时,若对于任意x∈[
| 1 |
| 2 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:①利用导数的几何意义,求出函数的解析式,再利用导数的正负,即可确定函数f(x)的单调区间.
②对于任意x∈[
,1]都有f(x)≥x恒成立,等价于m≥ex+
对于任意x∈[
,1]恒成立,求出函数的最大值,即可求实数m的最小值.
②对于任意x∈[
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
解答:
解:①f(x)=(mx+n)e-x,f′(x)=
∵函数f(x)在点(1,f(1))处的切线方程为x+ey-3=0,
∴f(1)=
,f′(1)=-
,
∴
,∴
,
∴f(x)=(x+1)e-x,
∴f′(x)=-
>0?x<0,f′(x)<0?x>0
∴f(x)的单调增区间为(-∞,0),单调减区间为(0,+∞)
②∵n=-1,m∈R,∴f(x)≥x?
≥x
对于任意x∈[
,1]都有f(x)≥x恒成立,等价于m≥ex+
对于任意x∈[
,1]恒成立
记g(x)=ex+
,则g′(x)=ex-
设h(x)=ex-
,h′(x)=ex+
>0对x∈[
,1]恒成立
∴h(x)=ex-
在[
,1]上单调递增,
又h(
)=
-4<0,h(1)=e-1>0,
∴g′(x)=ex-
在[
,1]上有唯一零点x0,
∴x∈(
,x0)时,g′(x)<0,x∈(x0,1)时,g′(x)>0,
∴g(x)的最大值是g(
)与g(1)中的较大的一个,
∵g(
)=
+2<g(1)=e+1,
∴m≥e+1,
∴实数m的最小值为e+1.
| -mx+m-n |
| ex |
∵函数f(x)在点(1,f(1))处的切线方程为x+ey-3=0,
∴f(1)=
| 2 |
| e |
| 1 |
| e |
∴
|
|
∴f(x)=(x+1)e-x,
∴f′(x)=-
| x |
| ex |
∴f(x)的单调增区间为(-∞,0),单调减区间为(0,+∞)
②∵n=-1,m∈R,∴f(x)≥x?
| mx-1 |
| ex |
对于任意x∈[
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
记g(x)=ex+
| 1 |
| x |
| 1 |
| x2 |
设h(x)=ex-
| 1 |
| x2 |
| 2 |
| x3 |
| 1 |
| 2 |
∴h(x)=ex-
| 1 |
| x2 |
| 1 |
| 2 |
又h(
| 1 |
| 2 |
| e |
∴g′(x)=ex-
| 1 |
| x2 |
| 1 |
| 2 |
∴x∈(
| 1 |
| 2 |
∴g(x)的最大值是g(
| 1 |
| 2 |
∵g(
| 1 |
| 2 |
| e |
∴m≥e+1,
∴实数m的最小值为e+1.
点评:本题考查的知识点是导数的几何意义,函数的单调性,函数的最值,其中将恒成立问题转化为最值问题是解答此类问题的关键.

练习册系列答案
相关题目
设α角的终边上一点P的坐标是(cos
,sin
),则α等于( )
| π |
| 5 |
| π |
| 5 |
A、
| ||
B、-
| ||
C、2kπ+
| ||
D、2kπ+
|
 如图,点A是单位圆与x轴正半轴的交点,点B(-
如图,点A是单位圆与x轴正半轴的交点,点B(-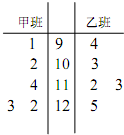 为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图:
为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图: