题目内容
设关于x的函数y=（k-2）x+1是R上的增函数，则实数k的取值范围是 ．
考点：函数单调性的性质
专题：函数的性质及应用
分析：直接利用一次函数时单调递增函数求出参数k的范围．
解答：
解：关于x的函数y=（k-2）x+1是R上的增函数
所以：k-2＞0
解得：k＞2
所以实数k的取值范围为：（2，+∞）
故答案为：（2，+∞）
所以：k-2＞0
解得：k＞2
所以实数k的取值范围为：（2，+∞）
故答案为：（2，+∞）
点评：本题考查的知识要点：一次函数单调性的应用．属于基础题型．
练习册系列答案
相关题目
函数y=f（x）是定义在R上的减函数，且f（1）=0，则满足f（lgx）＜0的解集为（ ）
| A、（0，1） | ||
B、（0，
| ||
| C、（10，+∞） | ||
| D、（1，+∞） |
执行如图所示的程序框图，若输入的n值等于7，则输出s的值为（ ）| A、15 | B、16 | C、21 | D、22 |
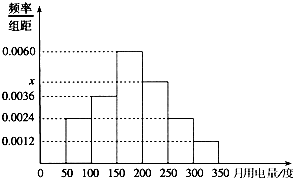
从某小区抽取100个家庭进行月用电量调查，发现其月用电量都在50度至350度之间，频率分布直方图如图所示．