题目内容
已知点P到两个定点M(-1,0)、N(1,0)距离的比为
,
(1)求动点P的轨迹方程;
(2)若点N到直线PM的距离为1.求直线PN的方程.
| 2 |
(1)求动点P的轨迹方程;
(2)若点N到直线PM的距离为1.求直线PN的方程.
考点:轨迹方程
专题:直线与圆
分析:(1)设出点P的坐标为(x,y),由题设有
=
,代入两点间的距离公式后整理得答案;
(2)由点N到PM的距离为1,结合|MN|=2可得∠PMN=30°,从而求得直线PM的斜率,写出直线PM的方程.联立直线方程和圆的方程求得P的坐标,然后由直线方程的两点式求得直线PN的方程.
| |PM| |
| |PN| |
| 2 |
(2)由点N到PM的距离为1,结合|MN|=2可得∠PMN=30°,从而求得直线PM的斜率,写出直线PM的方程.联立直线方程和圆的方程求得P的坐标,然后由直线方程的两点式求得直线PN的方程.
解答:
解:(1)设点P的坐标为(x,y),由题设有
=
,
即
=
.
整理得x2+y2-6x+1=0;
(2)∵点N到PM的距离为1,|MN|=2,
∴∠PMN=30°,直线PM的斜率为±
,
直线PM的方程为y=±
(x+1).
联立
,整理得x2-4x+1=0.
解得x=2±
.
代入y=-
(x+1),得点P的坐标为(2+
,-1-
)或(2-
,1-
);
联立
,求得点P的坐标为(2+
,1+
)或(2-
,-1+
).
∴直线PN的方程为y=x-1或y=-x+1.
| |PM| |
| |PN| |
| 2 |
即
| (x+1)2+y2 |
| 2 |
| (x-1)2+y2 |
整理得x2+y2-6x+1=0;
(2)∵点N到PM的距离为1,|MN|=2,
∴∠PMN=30°,直线PM的斜率为±
| ||
| 3 |
直线PM的方程为y=±
| ||
| 3 |
联立
|
解得x=2±
| 3 |
代入y=-
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
联立
|
| 3 |
| 3 |
| 3 |
| 3 |
∴直线PN的方程为y=x-1或y=-x+1.
点评:本题考查了圆的标准方程的求法,考查了直线和圆的位置关系,训练了由直线上的两点坐标求直线方程,是中档题.

练习册系列答案
相关题目
函数f(x)=
的值域是( )
|
| A、[-4,+∞) |
| B、[0,+∞) |
| C、[4,+∞) |
| D、(-∞,+∞) |
 甲、乙两家商场对同一种商品开展促销活动,两家商场对购买该商品的顾客奖励方案如下:
甲、乙两家商场对同一种商品开展促销活动,两家商场对购买该商品的顾客奖励方案如下: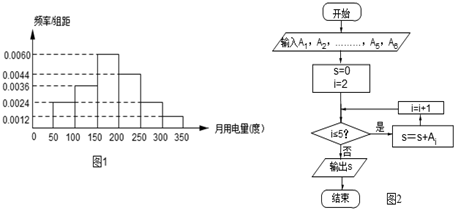
 函数f(x)=cos(πx+φ)(0<φ<
函数f(x)=cos(πx+φ)(0<φ<