题目内容
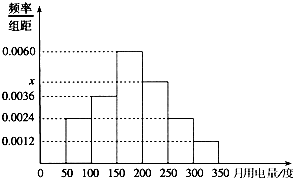
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图所示.在这些用户中,用电量落在区间[100,250)内的户数为 .

考点:频率分布直方图
专题:概率与统计
分析:根据频率分布直方图,结合频率、频数与样本容量的关系,求出答案即可.
解答:
解:根据频率分布直方图,得;
用电量落在区间[100,250)内的频率为:
1-0.0024×50-0.0024×50-0.0012×50=0.70,
∴用电量落在区间[100,250)内的户数为:
100×0.70=70.
故答案为:70.
用电量落在区间[100,250)内的频率为:
1-0.0024×50-0.0024×50-0.0012×50=0.70,
∴用电量落在区间[100,250)内的户数为:
100×0.70=70.
故答案为:70.
点评:本题考查了频率分布直方图的应用问题,也考查了频率=
的应用问题,是基础题目.
| 频数 |
| 样本容量 |

练习册系列答案
相关题目
一算法的程序框图如图1,若输出的y=
,则输入的x的值可能为( )

| 1 |
| 2 |

| A、-1 | B、0 | C、1 | D、5 |
已知l,m是两条不同的直线,α,β是两个不同的平面,则在下列条件中,一定能得到l⊥m的是( )
| A、α∩β=l,m与α,β所成角相等 |
| B、α⊥β,l⊥α,m∥β |
| C、l,m与平面α所成角之和为90° |
| D、α∥β,l⊥α,m∥β |
已知实数x,y满足
如果目标函数z=x-y的最小值为-1,则实数m等于( )
|
| A、7 | B、5 | C、4 | D、3 |
函数y=x+
(x>0)的递减区间为 ( )
| 4 |
| x |
| A、(0,4] |
| B、[2,4] |
| C、[2,+∞) |
| D、(0,2] |