题目内容
A、B、C、D、E五名实习老师被随机地分到甲、乙、丙、丁四个不同的学校实习，每个学校至少有一名实习老师．
（1）求A、B两人同时到甲学校实习的概率；
（2）求A、B两人不在同一个学校实习的概率．
（1）求A、B两人同时到甲学校实习的概率；
（2）求A、B两人不在同一个学校实习的概率．
考点：古典概型及其概率计算公式,排列、组合及简单计数问题
专题：概率与统计
分析：（1）先计算出A、B、C、D、E五名实习老师被随机地分到甲、乙、丙、丁四个不同的学校实习的基本事件总数，再计算A、B两人同时到甲学校实习的基本事件个数，代入古典概型概率计算公式，可得答案．
（2）利用对立事件概率减法公式，结合（1）中A、B两人同时到甲学校实习的概率，可得答案．
（2）利用对立事件概率减法公式，结合（1）中A、B两人同时到甲学校实习的概率，可得答案．
解答：
解：（1）A、B、C、D、E五名实习老师被随机地分到甲、乙、丙、丁四个不同的学校实习，
共有
•
=240种不同的分配方案，
记A、B两人同时到甲学校实习为事件E，
那么事件E包含的分配方案有：
=24种
即A、B两人同时到甲学校实习的概率P（E）=
=
．
（2）A、B两人不同在一学校实习为事件
，所
∴A、B两人不同在一学校实习的概率是1-P（E）=1-
=
共有
| C | 2 5 |
| A | 4 4 |
记A、B两人同时到甲学校实习为事件E，
那么事件E包含的分配方案有：
| A | 4 4 |
即A、B两人同时到甲学校实习的概率P（E）=
| 24 |
| 240 |
| 1 |
| 10 |
（2）A、B两人不同在一学校实习为事件
. |
| E |
∴A、B两人不同在一学校实习的概率是1-P（E）=1-
| 1 |
| 10 |
| 9 |
| 10 |
点评：本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．
练习册系列答案
相关题目
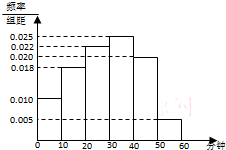电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查．如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图； 将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”