题目内容
证明4n≥n4（n为大于3的正整数）．将4换成其他更大的数试试，说说有什么规律．（禁用数学归纳法）
考点：不等式的证明
专题：证明题,导数的综合应用
分析：设y=
，求出导数，求出单调区间，则当x≥4且为整数时，有
≤
，化简整理，即可得证；将4换成其他更大的数，比如m，则mn≥nm（n≥m且n∈N）．
| lnx |
| x |
| lnx |
| x |
| ln4 |
| 4 |
解答：
证明：设y=
，则y′=
当x＞e时，y′＜0，y为减函数，当0＜x＜e时，y′＞0，y为增函数．
则当x≥4且为整数时，有
≤
，
即有4lnx≤xln4，即lnx4≤ln4x，
即有4x≥x4，
故有4n≥n4（n为大于3的正整数）．
将4换成其他更大的数，比如m，则mn≥nm（n≥m且n∈N）．
| lnx |
| x |
| 1-lnx |
| x2 |
当x＞e时，y′＜0，y为减函数，当0＜x＜e时，y′＞0，y为增函数．
则当x≥4且为整数时，有
| lnx |
| x |
| ln4 |
| 4 |
即有4lnx≤xln4，即lnx4≤ln4x，
即有4x≥x4，
故有4n≥n4（n为大于3的正整数）．
将4换成其他更大的数，比如m，则mn≥nm（n≥m且n∈N）．
点评：本题考查不等式的证明，考查导数的运用：判断函数的单调性，考查单调性的应用，以及对数函数的单调性，属于中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
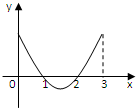函数f（x）定义域为[0，3]，导函数f′（x）在[0，3]内图象如图所示，则函数f（x）在[0，3]的单调递减区间为（ ）| A、[0，1] |
| B、[1，2] |
| C、[2，3] |
| D、[0，2] |
