题目内容
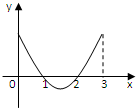函数f（x）定义域为[0，3]，导函数f′（x）在[0，3]内图象如图所示，则函数f（x）在[0，3]的单调递减区间为（ ）| A、[0，1] |
| B、[1，2] |
| C、[2，3] |
| D、[0，2] |
考点：利用导数研究函数的单调性,导数的运算
专题：导数的概念及应用
分析：根据导数和函数的单调性的关系即可判断，导数大于0，函数为增函数，导数小于0，函数为减函数
解答：
解∵f（x）的导函数y=f′（x）的图象如图所示：
∴观察图象知：在区间[1，2]内，f′（x）＜0，
∴f（x）的单调递减区间是[1，2]，
故选：B
∴观察图象知：在区间[1，2]内，f′（x）＜0，
∴f（x）的单调递减区间是[1，2]，
故选：B
点评：本题考查函数的单调区间和极大值的求法，解题时要认真审题，仔细观察图象，熟练掌握导数的应用．
练习册系列答案
相关题目
在△ABC中，sin2A+sin2B+sin2C=2
sinAsinBsinC，则△ABC的形状是（ ）
| 3 |
| A、直角三角形 |
| B、等腰直角三角形 |
| C、钝角三角形 |
| D、正三角形 |
设函数f（x）=x2+ax+b．若f（1）≤2，f（-1）≤2，f（0）≥0，则f（2）的最大值为（ ）
| A、-2 | B、6 | C、7 | D、10 |
若a是从区间[-2，2]任取的一个数，b是从区间[-2，2]任取的一个数，则关于x的一元二次方程x2+2ax-（b2-1）=0有实根的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|