题目内容
4.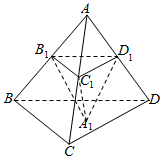 如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )| A. | 当x=$\frac{2}{3}$时,函数f(x)取到最大值 | |
| B. | 函数f(x)在($\frac{1}{2}$,1)上是减函数 | |
| C. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| D. | 存在x0,使得f(x0)$>\frac{1}{3}{V}_{A-BCD}$(其中VA-BCD为四面体ABCD的体积) |
分析 由题意求出平面B1C1D1的面积,求出平面B1C1D1与平面BCD的距离,代入三棱锥体积公式求得函数V=f(x),然后利用导数求其单调区间和最值,逐一核对四个选项得答案.
解答  解:如图,∵四面体ABCD是棱长为a的正四面体,
解:如图,∵四面体ABCD是棱长为a的正四面体,
∴顶点A在底面的射影为底面正三角形的中心,设为O,
则BO为正三角形BCD底边CD中线的$\frac{2}{3}$,即BO=$\frac{2}{3}×\sqrt{{a}^{2}-(\frac{a}{2})^{2}}=\frac{\sqrt{3}}{3}a$,
∴正四面体的高为h=$\sqrt{{a}^{2}-(\frac{\sqrt{3}}{3}a)^{2}}=\frac{\sqrt{6}}{3}a$.
∵平面B1C1D1∥平面BCD,∴△B1C1D1∽△BCD,
又$\frac{A{D}_{1}}{AD}$=x,∴$\frac{{S}_{△{B}_{1}{C}_{1}{D}_{1}}}{{S}_{△BCD}}={x}^{2}$,
又${S}_{△BCD}=\frac{1}{2}×a×\frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{4}{a}^{2}$,
∴${S}_{△{B}_{1}{C}_{1}{D}_{1}}=\frac{\sqrt{3}}{4}{a}^{2}{x}^{2}$,
设A到平面B1C1D1的距离为h′,由$\frac{h′}{h}=x$,得$h′=\frac{\sqrt{6}}{3}ax$,
∴平面B1C1D1与平面BCD间的距离,即A1到平面B1C1D1的距离为$\frac{\sqrt{6}}{3}a(1-x)$.
则V=$\frac{1}{3}×\frac{\sqrt{3}}{4}{a}^{2}{x}^{2}×\frac{\sqrt{6}}{3}a(1-x)$=$\frac{\sqrt{2}}{12}{a}^{2}({x}^{2}-{x}^{3})$(0<x<1),
V′=$\frac{\sqrt{2}}{12}{a}^{2}(2x-3{x}^{2})$,由V′=0,得x=$\frac{2}{3}$,
当x∈(0,$\frac{2}{3}$)时,V′>0,当x∈($\frac{2}{3},1$)时,V′<0,
∴当x=$\frac{2}{3}$时,V有最大值等于$\frac{\sqrt{2}}{81}{a}^{2}$..
故A正确,B,C错误,
又$\frac{1}{3}{V}_{A-BCD}=\frac{1}{3}×\frac{\sqrt{3}}{4}{a}^{2}×\frac{\sqrt{6}}{3}a=\frac{\sqrt{2}}{12}{a}^{3}$,
∴不存在x0,使得f(x0)$>\frac{1}{3}{V}_{A-BCD}$,D错误.
故选:A.
点评 本题考查棱锥体积的求法,训练了利用导数研究函数的单调性,考查了利用导数求函数的最值,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $[{-1,\frac{1}{2}})∪[{2,+∞})$ | B. | $[{-1,\frac{1}{2}}]∪({2,+∞})$ | C. | [2,+∞) | D. | $[{-1,\frac{1}{2}})$ |
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
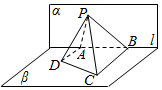 如图,已知平面α∩平面β=l,α⊥β.A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )
如图,已知平面α∩平面β=l,α⊥β.A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )| A. | 48 | B. | 16 | C. | $24\sqrt{3}$ | D. | 144 |
| A. | $\frac{3}{8}$ | B. | 2 | C. | 6 | D. | $\frac{2}{3}$ |
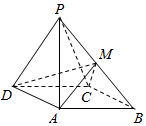 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点. 如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.
如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.