题目内容
13.在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C.(1)求角B的大小;
(2)若$a=c=\sqrt{3}$,求b的值.
分析 (1)根据正弦定理和两角和的正弦公式,根据特殊角的三角函数值即可求出,
(2)根据余弦定理求出b即可
解答 解:(1)因为(2a-c)cos B=bcos C,由正弦定理,得
(2sin A-sin C)cos B=sin Bcos C,
即2sin Acos B=sin Ccos B+sin Bcos C=sin(C+B)=sin A.
在△ABC中,0<A<π,sin A>0,
所以cos B=$\frac{1}{2}$.
又因为0<B<π,
故B=$\frac{π}{3}$.
(2)因为$a=c=\sqrt{3}$,由余弦定理得b2=a2+c2-2accos B,
所以b2=3.
所以$b=\sqrt{3}$.
点评 本题考查正余弦定理的应用,涉及三角函数的恒等变形,关键是熟悉三角函数的恒等变形的公式.

练习册系列答案
相关题目
3.血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
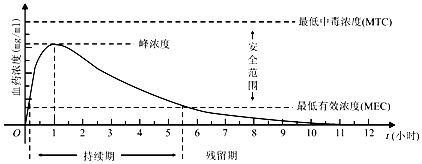
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是( )

根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是( )
| A. | 首次服用该药物1单位约10分钟后,药物发挥治疗作用 | |
| B. | 每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒 | |
| C. | 每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用 | |
| D. | 首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒 |
1.函数f(x)=3x-x2的零点所在区间是( )
| A. | (1,2) | B. | (0,1) | C. | (-1,0) | D. | (-2,-1) |
8.在△ABC中,内角A,B,C所对的边分别为a,b,c,A=$\frac{π}{4}$,b2-a2=c2,则tan C等于( )
| A. | 1 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
18.若z(1+i)=2i则|z|等于( )
| A. | 3 | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2 |
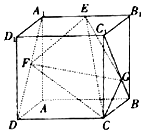 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为线段A1B1的中点,点F,G分别是线段A1D与BC1上的动点,当三棱锥E-FGC的俯视图的面积最大时,该三棱锥的正视图的面积是2.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为线段A1B1的中点,点F,G分别是线段A1D与BC1上的动点,当三棱锥E-FGC的俯视图的面积最大时,该三棱锥的正视图的面积是2.