已知α.β是两个不同平面.直线l?β.则“α∥β 是“l∥α 的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件题目和参考答案——青夏教育精英家教网—

题目内容

10．已知α，β是两个不同平面，直线l?β，则“α∥β”是“l∥α”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

分析 α，β是两个不同平面，直线l?β，则“α∥β”⇒“l∥α”，反之不成立．即可得出结论．

解答解：∵α，β是两个不同平面，直线l?β，则“α∥β”⇒“l∥α”，反之不成立．
∴α，β是两个不同平面，直线l?β，则“α∥β”是“l∥α”的充分不必要条件．
故选：A．

点评本题考查了线面面面平行的判定与性质定理、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．

练习册系列答案

$\frac{x^2}{2}-{y^2}$=1（x≠±$\sqrt{2}$）

B．

$\frac{x^2}{2}-{y^2}$=1

C．

$\frac{x^2}{2}+{y^2}$=1（y≠0）

D．

$\frac{y^2}{2}+{x^2}$=1

1．已知函数f（x）=sin（2x+$\frac{π}{6}$）+$\frac{1}{2}$
（1）画出函数f（x）在[-$\frac{π}{12}$，$\frac{11π}{12}$]上的简图．
（2）若x∈[-$\frac{π}{6}$，$\frac{π}{3}$]，函数g（x）=f（x）+m的最小值为2，求函数g（x）在该区间的最大值及取得最大值时x的值．

18．函数$f（x）=\sqrt{-{x^2}+（a+2）x-a-1}（a＞0）$的定义域为集合A，函数g（x）=2^x-1（x≤2）的值域为集合B．
（1）当a=1时，求集合A，B；
（2）若集合A，B满足A∪B=B，求实数a的取值范围．

5．若点A的坐标是（3，2），F是抛物线y²=2x的焦点，点P在抛物线上移动，为使得|PA|+|PF|取得最小值，则P点的坐标是（　　）

15．已知向量$\overrightarrow a=（3，\sqrt{3}）$，$\overrightarrow b=（0，x）$，若$\overrightarrow a•\overrightarrow b=|\overrightarrow a|$，则实数x=2．

2．设m，n是两条不同的直线，α，β是两个不同的平面（　　）

19．在△ABC中，∠C=45°，O是△ABC的外心，若$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}（{m，n∈R}）$，则m+n的取值范围为[-$\sqrt{2}$，1）．

20．

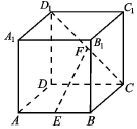正方体ABCD-A₁B₁C₁D₁中，E为AB中点，F为CD₁中点．
（1）求证：EF∥平面ADD₁A₁；
（2）AB=2，求三棱锥D₁-DEF的体积．

试题分类