题目内容
8.某化工厂每一天中污水污染指数f(x)与时刻x(时)的函数关系为f(x)=|log25(x+1)-a|+2a+1,x∈[0,24],其中a为污水治理调节参数,且a∈(0,1).(1)若$a=\frac{1}{2}$,求一天中哪个时刻污水污染指数最低;
(2)规定每天中f(x)的最大值作为当天的污水污染指数,要使该厂每天的污水污染指数不超过3,则调节参数a应控制在什么范围内?
分析 (1)通过$a=\frac{1}{2}$,化简$f(x)=|{{{log}_{25}}({x+1})-\frac{1}{2}}|+2≥2$,求出x=4.得到一天中早上4点该厂的污水污染指数最低.
(2)设t=log25(x+1),设g(t)=|t-a|+2a+1,t∈[0,1],得到$g(t)=\left\{\begin{array}{l}-t+3a+1,0≤t≤a\\ t+a+1,a<t≤1\end{array}\right.$,利用分段函数,函数的单调性最值求解即可.
解答 解:(1)因为$a=\frac{1}{2}$,则$f(x)=|{{{log}_{25}}({x+1})-\frac{1}{2}}|+2≥2$.…(2分)
当f(x)=2时,${log_{25}}({x+1})-\frac{1}{2}=0$,得$x+1={25^{\frac{1}{2}}}=5$,
即x=4.所以一天中早上4点该厂的污水污染指数最低.…(4分)
(2)设t=log25(x+1),则当0≤x≤24时,0≤t≤1.
设g(t)=|t-a|+2a+1,t∈[0,1],
则$g(t)=\left\{\begin{array}{l}-t+3a+1,0≤t≤a\\ t+a+1,a<t≤1\end{array}\right.$,…(7分)
显然g(t)在[0,a]上是减函数,在[a,1]上是增函数,
则f(x)max=max{g(0),g(1)},…(9分)
因为g(0)=3a+1,g(1)=a+2,
则有 $\left\{{\begin{array}{l}{g(0)=3a+1≤3}\\{g(1)=a+2≤3}\end{array}}\right.$,解得$a≤\frac{2}{3}$,…(11分)
又a∈(0,1),故调节参数a应控制在$(0,\frac{2}{3}]$内.…(12分)
点评 本题考查函数的实际应用,分段函数的应用,考查函数的单调性以及函数的最值的求法,考查计算能力.

| A. | $\frac{{2\sqrt{2}}}{81}π$ | B. | $\frac{{4\sqrt{5}}}{81}π$ | C. | $\frac{8}{81}π$ | D. | $\frac{10}{81}π$ |
| A. | 53,50 | B. | 53,30 | C. | 3,50 | D. | 3,31 |
| A. | -$\frac{3}{4}$ | B. | -1 | C. | $\frac{3}{2}$ | D. | 2 |
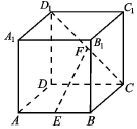 正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.
正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.