题目内容
圆x2+y2+2x-4y-6=0的圆心和半径分别是（ ）
| A、（-1，-2），11 | ||
| B、（-1，2），11 | ||
C、（-1，-2），
| ||
D、（-1，2），
|
考点：圆的一般方程
专题：直线与圆
分析：将题中的圆化成标准方程得（x+1）2+（y-2）2=11，由此即可得到圆心的坐标和半径．
解答：
解：将圆x2+y2+2x-4y-6=0化成标准方程，
得（x+1）2+（y-2）2=11，
∴圆心的坐标是（-1，2），半径r=
．
故选D．
得（x+1）2+（y-2）2=11，
∴圆心的坐标是（-1，2），半径r=
| 11 |
故选D．
点评：本题给出定圆，求圆心C的坐标．着重考查了圆的标准方程和基本概念等知识，属于基础题．
练习册系列答案
阶梯计算系列答案
相关题目
若
=（a1，a2，a3），
=（b1，b2，b3），则
=
=
是
∥
的（ ）
| a |
| b |
| a1 |
| b1 |
| a2 |
| b2 |
| a3 |
| b3 |
| a |
| b |
| A、既不充分也不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、充分不必要条件 |
“a＜2”是“对任意实数x，|x+1|+|x-1|≥a成立”的（ ）
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
设P是椭圆
+
=1上一点，F1、F2是椭圆的焦点，若|PF1|等于4，则|PF2|等于（ ）
| x2 |
| 169 |
| y2 |
| 144 |
| A、22 | B、21 | C、20 | D、13 |
△ABC 中，
=
，则△ABC一定是（ ）
| 1-cosA |
| 1-cosB |
| a |
| b |
| A、钝角三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、等腰三角形 |
在△ABC中，A=
，C=
，b=2，则此三角形的最小边长是（ ）
| π |
| 3 |
| π |
| 6 |
| A、1 | ||||
B、2
| ||||
C、
| ||||
D、
|
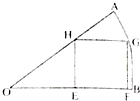如图所示，扇形OAB中，∠AOB=