题目内容
2．多面体的三视图如图所示，则该多面体的表面积为$\frac{32}{3}$cm2．
分析 如图所示，由三视图可知：该几何体为三棱锥P-ABC．该几何体可以看成是两个底面均为△PCD，高分别为AD和BD的棱锥形成的组合体，进而可得答案．
解答 解：如图所示，
由三视图可知：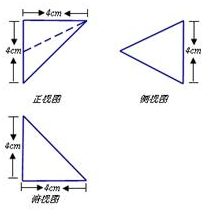
该几何体为三棱锥P-ABC．
该几何体可以看成是两个底面均为△PCD，高分别为AD和BD的棱锥形成的组合体，
由几何体的俯视图可得：△PCD的面积S=$\frac{1}{2}$×4×4=8cm2，
由几何体的正视图可得：AD+BD=AB=4cm，
故几何体的体积V=$\frac{1}{3}$×8×4=$\frac{32}{3}$cm3，
故答案为：$\frac{32}{3}$．
点评 本题考查由三视图求几何体的体积和表面积，根据已知的三视图分析出几何体的形状是关键．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1．已知数列{an}满足${a_1}=2，{a_{n+1}}=\frac{{{a_n}-1}}{{{a_n}+1}}（n∈N*）$，则该数列的前2017项的乘积a1a2a3…a2017=（ ）
| A． | 2 | B． | $\frac{1}{3}$ | C． | -$\frac{1}{3}$ | D． | -2 |
13．已知定义在R上的奇函数f（x）和偶函数g（x）满足：f（x）+g（x）=ex，则（ ）
| A． | $f（x）=\frac{{{e^x}+{e^{-x}}}}{2}$ | B． | $f（x）=\frac{{{e^x}-{e^{-x}}}}{2}$ | C． | $g（x）=\frac{{{e^x}-{e^{-x}}}}{2}$ | D． | $g（x）=\frac{{{e^{-x}}-{e^x}}}{2}$ |
14．已知全集U=R，集合A={x|x＞2或x＜1}，B={x|x-a≤0}，若∁UB⊆A，则实数a的取值范围是（ ）
| A． | （1，+∞） | B． | [1，+∞） | C． | （2，+∞） | D． | [2，+∞） |
11．已知α，β为锐角，且cosα=$\frac{3}{5}$，sin（α-β）=$\frac{5}{13}$，则cosβ=（ ）
| A． | -$\frac{16}{65}$ | B． | $\frac{56}{65}$ | C． | $\frac{16}{65}$ | D． | -$\frac{56}{65}$ |