题目内容
7.已知函数f(x)=4cosxsin(x+$\frac{π}{6}$)-1(Ⅰ)求f(x)的周期和单调减区间;
(Ⅱ)求f(x)在区间[-$\frac{π}{6},\frac{π}{4}$]上的取值范围.
分析 (Ⅰ)先利用辅助角公式或二倍角和两角和余差的基本公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期,最后将内层函数看作整体,放到正弦函数的减区间上,解不等式得函数的单调递减区间;
(Ⅱ)x在[-$\frac{π}{6},\frac{π}{4}$]上,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的取值最大和最小值,即得到f(x)的取值范围.
解答 解:函数f(x)=4cosxsin(x+$\frac{π}{6}$)-1
化简可得:f(x)=4cosxsinxcos$\frac{π}{6}$+4cosx•cosxsin$\frac{π}{6}$-1=$2\sqrt{3}$sinxcosx+2cos2x-1=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$)
(Ⅰ)f(x)的周期T=$\frac{2π}{ω}=\frac{2π}{2}=π$.
令2kπ$+\frac{π}{2}$≤2x$+\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,解得:kπ$+\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,(k∈Z);
∴f(x)的单调递增区间为[kπ$+\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z);
(Ⅱ):x在[-$\frac{π}{6},\frac{π}{4}$]上,
∴2x$+\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{2π}{3}$],
可得:sin(2x+$\frac{π}{6}$)∈[$-\frac{1}{2}$,1].
故f(x)∈[-1,2],
∴f(x)在区间[-$\frac{π}{6},\frac{π}{4}$]上的取值范围是[-1,2].
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | y=log${\;}_{\frac{1}{2}}$x | B. | y=x-1 | C. | y=($\frac{1}{2}$)x | D. | y=x2 |
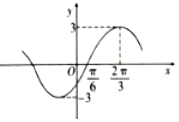
| A. | $y=3sin({2x-\frac{π}{6}})$ | B. | $y=3sin({2x-\frac{π}{3}})$ | C. | $y=3sin({x-\frac{π}{6}})$ | D. | $y=3sin({x-\frac{π}{3}})$ |
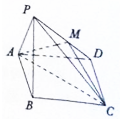 如图,已知四棱锥P-ABCD,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.