题目内容
12．已知圆M：x2+y2-2ax=0（a＜0）截直线x-y=0所得线段的长度是$2\sqrt{2}$，则圆M与圆N：（x-2）2+（y-1）2=9的位置关系是（ ）| A． | 内切 | B． | 相交 | C． | 外切 | D． | 相离 |
分析 根据直线与圆相交的弦长公式，求出a的值，结合两圆的位置关系进行判断即可．
解答 解：圆M圆心坐标为（a，0），由题意得${a^2}={（{\frac{|a|}{{\sqrt{2}}}}）^2}+{（{\sqrt{2}}）^2}$且a＜0，解得a=-2，
则$1＜|{MN}|=\sqrt{17}＜5$，
故选B．
点评 本题主要考查直线和圆相交的应用，以及两圆位置关系的判断，根据相交弦长公式求出a的值是解决本题的关键．
练习册系列答案
相关题目
3．将二次函数y=x2的图象向下平移1个单位，则平移后的二次函数的解析式为（ ）
| A． | y=x2-1 | B． | y=x2+1 | C． | y=（x-1）2 | D． | y=（x+1）2 |
17．函数$y=Asin（{ωx+φ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，则（ ）
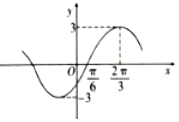
| A． | $y=3sin（{2x-\frac{π}{6}}）$ | B． | $y=3sin（{2x-\frac{π}{3}}）$ | C． | $y=3sin（{x-\frac{π}{6}}）$ | D． | $y=3sin（{x-\frac{π}{3}}）$ |
2．
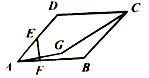如图所示，四边形ABCD是菱形，边长为2，∠BAD=60°，E为边AD的中点，点F在边AB上运动，点A关于直线EF的对称点为G，则线段CG的长度最小值为（ ）
如图所示，四边形ABCD是菱形，边长为2，∠BAD=60°，E为边AD的中点，点F在边AB上运动，点A关于直线EF的对称点为G，则线段CG的长度最小值为（ ）| A． | $\sqrt{7}-1$ | B． | 2 | C． | $\sqrt{5}-1$ | D． | $\sqrt{3}$ |