题目内容

14．已知全集U=R，集合A={x|x＞2或x＜1}，B={x|x-a≤0}，若∁UB⊆A，则实数a的取值范围是（　　）
A．（1，+∞）B．[1，+∞）C．（2，+∞）D．[2，+∞）

分析 利用不等式的解法即可化简集合A，B，再利用集合的运算即可．

解答 解：∵集合A={x|x＞2或x＜1}，B={x|x-a≤0}，
∴CUB=（a，+∞）．
∵∁UB⊆A，
∴a≥2．
∴实数a的取值范围是[2，+∞）．
故选D．

点评 本题考查了一元二次不等式的解法、集合的运算性质，属于基础题．

练习册系列答案
相关题目
4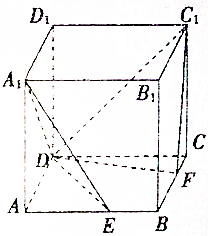．如图所示，ABCD-A1B1C1D1是棱长为6的正方体，E，F分别是棱AB，BC上的动点，且AE=BF．当A1，E，F，C1共面时，平面A1DE与平面C1DF所成锐二面角的余弦值为（　　）
A．$\frac{\sqrt{3}}{2}$B．$\frac{1}{2}$C．$\frac{1}{5}$D．$\frac{2\sqrt{6}}{5}$
5．若数x，y满足$\left\{{\begin{array}{l}{x-y+1≥0}\\{x+y-3≥0}\\{2x+y-7≤0}\end{array}}\right.$，则z=x-2y的最小值是（　　）
A．-3B．-4C．6D．-6
2．多面体的三视图如图所示，则该多面体的表面积为$\frac{32}{3}$cm2．
9．化简：
（1）sin（$\frac{π}{6}$-2π）cos（$\frac{π}{4}$+π）
（2）sin（$\frac{π}{4}$+$\frac{5π}{2}$）
19．若函数f（x）对任意实数x，y均有f（x）•f（y）=f（x+y），且对于任意的x都有f（x）＞0，且当x＜0时f（x）＞1．
（1）求证：f（x）为R上的减函数；
（2）当f（4）=$\frac{1}{16}$时，若f（x2-3x+2）≤$\frac{1}{4}$，求实数x的取值范围．
6．△ABC中，AB=6，AC=8，∠BAC=90°，△ABC所在平面α外一点P到点A、B、C的距离都是13，则P到平面α的距离为（　　）
A．7B．9C．12D．13
3．将二次函数y=x2的图象向下平移1个单位，则平移后的二次函数的解析式为（　　）
A．y=x2-1B．y=x2+1C．y=（x-1）2D．y=（x+1）2
4．已知向量$\overrightarrow a=（4，-2）$，$\overrightarrow b=（x，1）$，若$\overrightarrow a∥\overrightarrow b$，则$|\overrightarrow a+\overrightarrow b|$=$\sqrt{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网