题目内容
13.已知定义在R上的奇函数f(x)和偶函数g(x)满足:f(x)+g(x)=ex,则( )| A. | $f(x)=\frac{{{e^x}+{e^{-x}}}}{2}$ | B. | $f(x)=\frac{{{e^x}-{e^{-x}}}}{2}$ | C. | $g(x)=\frac{{{e^x}-{e^{-x}}}}{2}$ | D. | $g(x)=\frac{{{e^{-x}}-{e^x}}}{2}$ |
分析 将已知等式的x换成-x,结合在R上的奇函数f(x)和偶函数g(x),利用方程组的思想解出f(x)的解析式.
解答 解:由已知:在R上的奇函数f(x)和偶函数g(x),f(x)+g(x)=ex,①
所以f(-x)+g(-x)=e-x,即-f(x)+g(x)=e-x,②
①②得f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$;
故选B.
点评 本题考查了利用方程思想求函数解析式;关键是正确利用两个函数的奇偶性.

练习册系列答案
相关题目
4.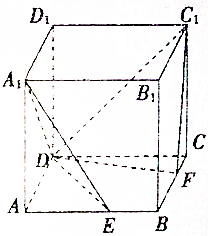 如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )
 如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{2\sqrt{6}}{5}$ |
8.在(2x+a)5的展开式中,含x2项的系数等于320,则$\int_0^a{({e^x}+2x)dx}$等于( )
| A. | e2+3 | B. | e2+4 | C. | e+1 | D. | e+2 |
5.若数x,y满足$\left\{{\begin{array}{l}{x-y+1≥0}\\{x+y-3≥0}\\{2x+y-7≤0}\end{array}}\right.$,则z=x-2y的最小值是( )
| A. | -3 | B. | -4 | C. | 6 | D. | -6 |
3.将二次函数y=x2的图象向下平移1个单位,则平移后的二次函数的解析式为( )
| A. | y=x2-1 | B. | y=x2+1 | C. | y=(x-1)2 | D. | y=(x+1)2 |
