题目内容

设定义在（0，
π
2
）上的函数y=2sinx的图象分别与y=cosx，y=tanx的图象交于点（x1，y1），（x2，y2），则
5
y1+y2=（　　）
A、3+
2
B、2+
2
C、3+
3
D、2+
3
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：利用已知条件求出y1，y2，然后求解
5
y1+y2的值即可．
解答： 解：定义在（0，
π
2
）上的函数y=2sinx的图象分别与y=cosx，y=tanx的图象交于点（x1，y1），（x2，y2），
∴2sinx=cosx，∴y12=4sin2x1=
4sin2x
sin2x+cos2x
=
4
5
，
∴y1=
2
5
．
2sinx=tanx，∴cosx=
1
2
，x=
π
3
，
y2=tan
π
3
=
3
．
5
y1+y2=
5
×
2
5
+
3
=2+
3
．
故选：D．
点评：本题考查三角函数方程是解法，函数的图象与形状，基本知识的综合应用．
练习册系列答案
相关题目
高三年级有8名语文教师，其中2男6女，每位老师代两个班．现从中任选1男2女担任辩论赛决赛评委，规定本班任课教师不能担任本班比赛时的评委．已知进入八强的班级任课教师均为女性，则选取决赛评委的办法有
 
种．
若f（x）是定义在R上的偶函数，则f（1+
2
）-f（
1
1-
2
）=
 
．
给出以下四个命题，其中所有正确命题的序号为：
 
．
（1）“b2=ac”是“实数a、b、c成等比数列”的必要而不充分条件；
（2）已知线性回归方程
∧
y
=3+2x，当变量x增加2个单位，其预报值
∧
y
平均增加4个单位；
（3）函数f（x）=ex-（
1
2
）x在区间（-1，1）上只有1个零点；
（4）命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠1，则x2-3x+2=0”；
（5）设随机变量ξ服从正态分布N（2，9），若P（ξ＞c+1）=P（ξ＜c-1），则c等于3．
若复数z满足iz=2+4i，则在复平面内，z的共轭复数
.
z
对应的点的坐标是（　　）
A、（2，4）
B、（2，-4）
C、（4，-2）
D、（4，2）
若a＞0，b＞0，则不等式-b＜
1
x
＜a的解集为（　　）
A、{x|-
1
a
＜x＜0或0＜x＜
1
b
}
B、{x|-
1
b
＜x＜0或0＜x＜
1
a
}
C、{x|x＜-
1
a
或x＞
1
b
}
D、{x|x＜-
1
b
或x＞
1
a
}
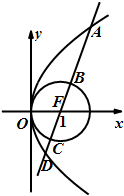已知抛物线y2=4x，圆F：（x-1）2+y2=1，过点F作直线l，自上而下顺次与上述两曲线交于点A，B，C，D（如图所示），则|AB|•|CD|的值正确的是（　　）
A、等于1B、最小值是1
C、等于4D、最大值是4
已知函数f（x）=
2x      (x＜0)
log2x (x＞0)
若直线y=m与函数f（x）的图象有两个不同的交点，则实数m的取值范围是（　　）
A、m∈RB、m＞1
C、m＞0D、0＜m＜1
已知函数f（x）=ex-2x+a有零点，则实数a的取值范围是（　　）
A、（-∞，2ln2-2]
B、[2ln2-2，+∞）
C、[2ln2，+∞）
D、[2ln2-2，2ln2]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网